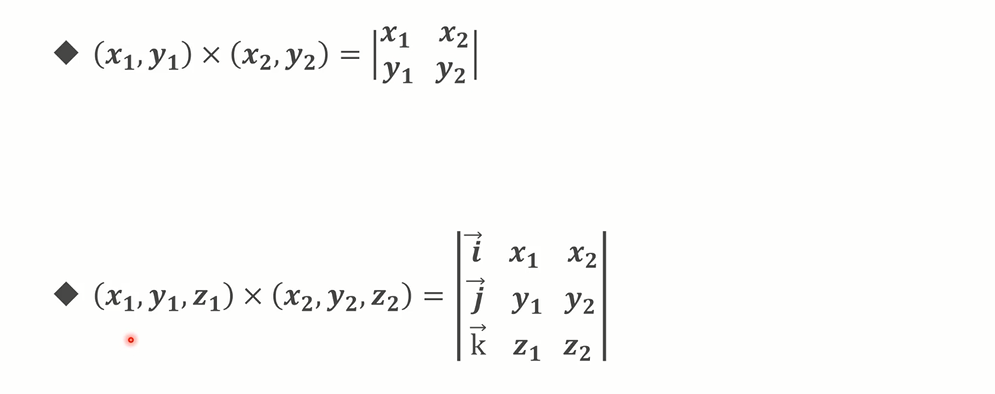# 向量
# 什么是向量
指具有大小(magnitude)和方向的量。它可以形象化地表示为带箭头的线段;箭头所指:代表向量的方向;线段长度:代表向量的大小。与向量对应的量叫做数量(物理学中称标量),数量(或标量)只有大小,没有方向。
可以看做空间中的一个点,可以看做从原点指向这个点的一个方向; 向量可以从两个视角去看:这两个视角,都是不是简单的一组数据;
- 一个是一个有向线段
- 一个是空间中的点
我们一般提到向量,都是指列向量;
# 三维直角坐标系
- 直角坐标系也叫笛卡尔坐标系
- 原本的二维坐标系(x,y 轴),再增加一个垂直的 z 轴
- z 轴方向不同分成右手系和左手系
三维空间向量
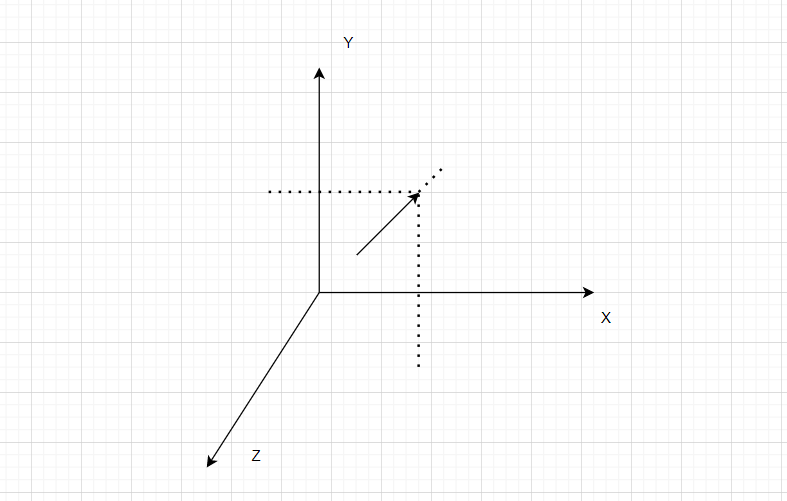
# 向量的表示
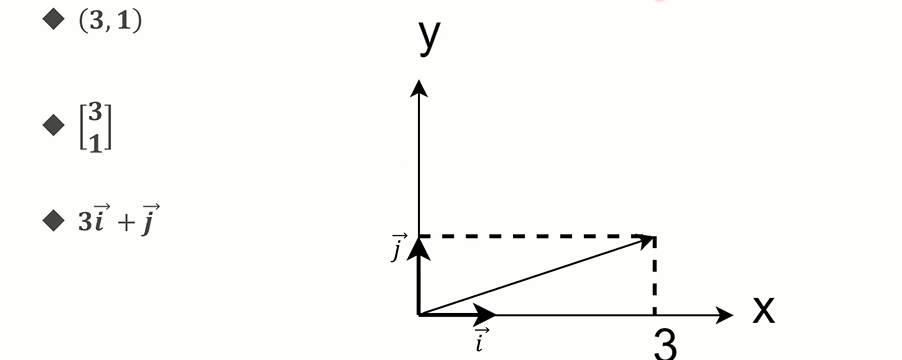
- 二维
第一种是通常向量的表示,应该在数字的上方带一个箭头,用来区分向量,第二种是通过矩阵来表示,第三种是单位向量来表示。
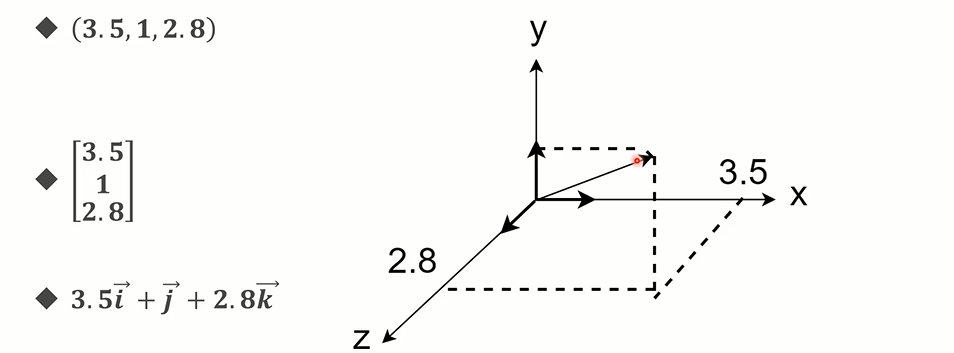
- 三维
# 向量乘以常数
- 向量乘以常数:向量乘以常数可以看到向量被成倍延长了;负数倍数会返过来:

# 向量加法
数学上计算就是对应的分量进行相加
(5, 2)T + (2, 5)T = (7, 7)T
就是先向 x 移动 5 个单位,再向 y 移动 2 个单位;然后再向 x 移动 2 个单位,再向 y 移动 5 个单位;就是一个平行四边形的对角线的长度;
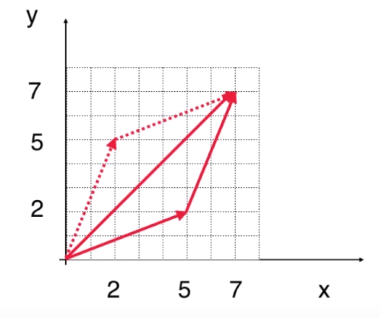
三维也是一样的:
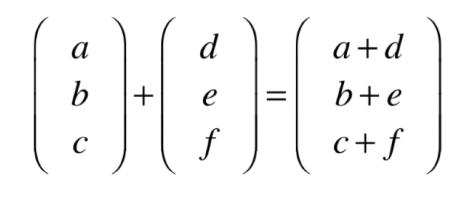
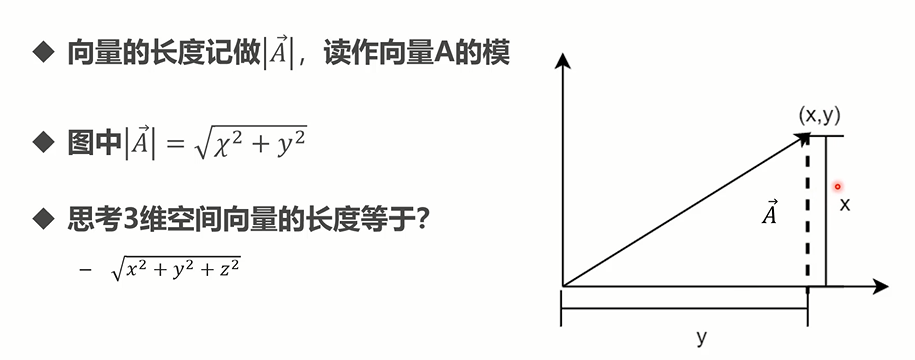
# 向量的长度

# 向量的基本性质
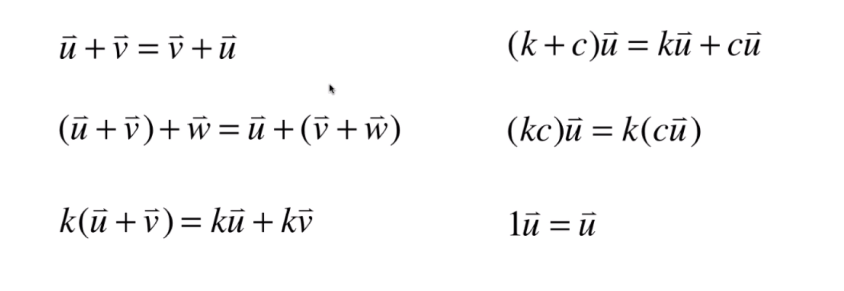
# 零向量
也就是任意一个向量 U,都存在一个向量 O,满足 U + O = U;则 O 成为零向量;也就是由 0 组成的向量;也就是各个维度都为 0 的向量;这个 O 是没有箭头的;因为箭头表示方向;O 向量是没有方向的;

# 单位向量
单位向量只表示方向;他的模也就是他的长度为 1:

单位向量有无数个;
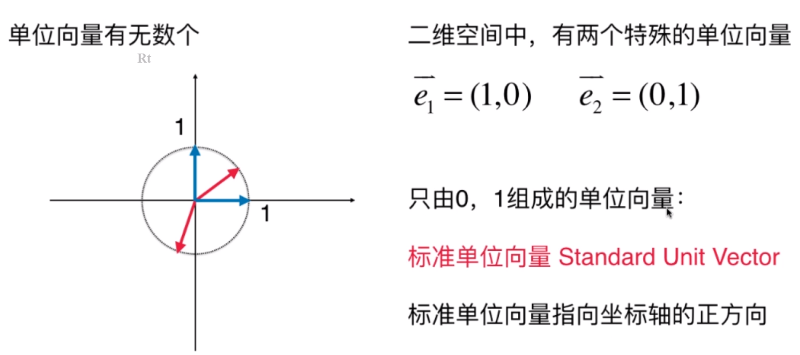
标准单位向量就是说有一个维度为 1 的向量。三维中就是有三个标准单位向量:(1, 0, 0)、(0, 1, 0)、(0, 0, 1); 我们整个空间的坐标系就是由标准单位向量来组建的;
# 向量相乘(点积、内积)
- 两个向量相乘结果是一个数:
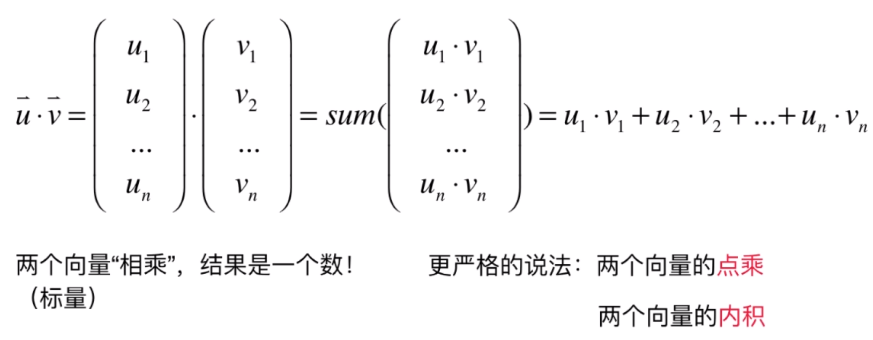
- 其他计算方式:
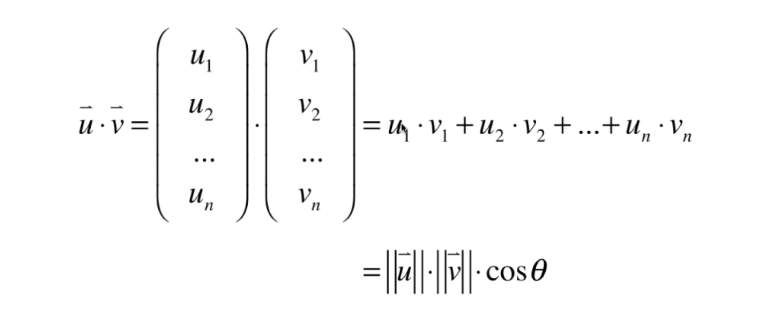
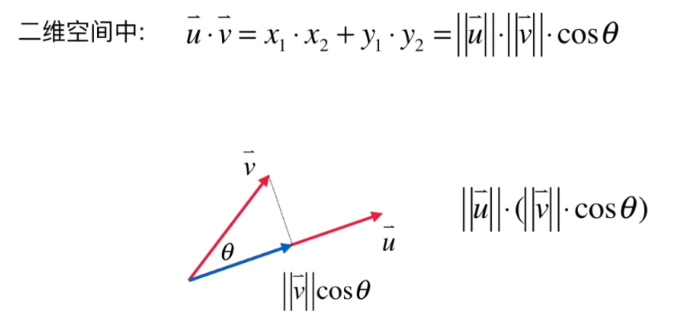
公式推导如下: 主要用到余弦定理:已知三条边跟两条边的夹角;
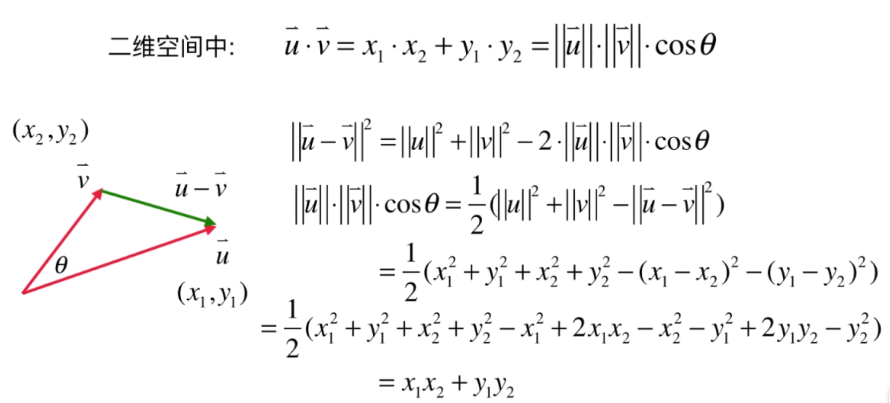
几何意义:
就是说,将其中一个向量投影到另一个向量上(或者把两个向量都投影到 x、y 坐标轴上),因为向量表达方向大小。只有在同方向的两个向量计算才是有意义的,所以;最终的结果就是一个向量在另一个向量上的投影的长度乘以另一个向量的长度;
- 点乘的应用
- 可以计算两个向量的夹角;

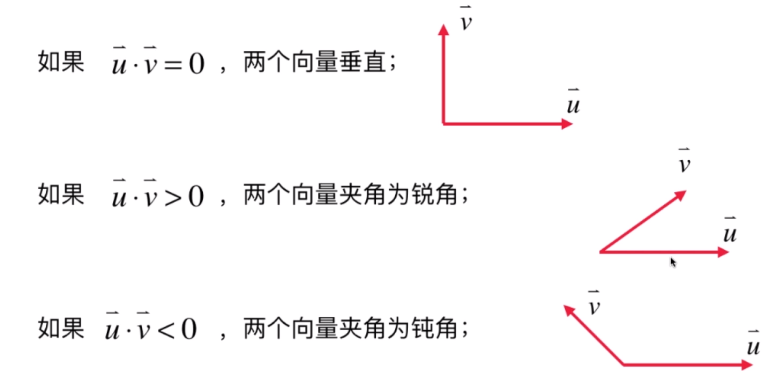
- 计算一个向量投影在另一个向量的投影点的向量

# 线性组合
- 二维
前提是两个向量不是平行的。
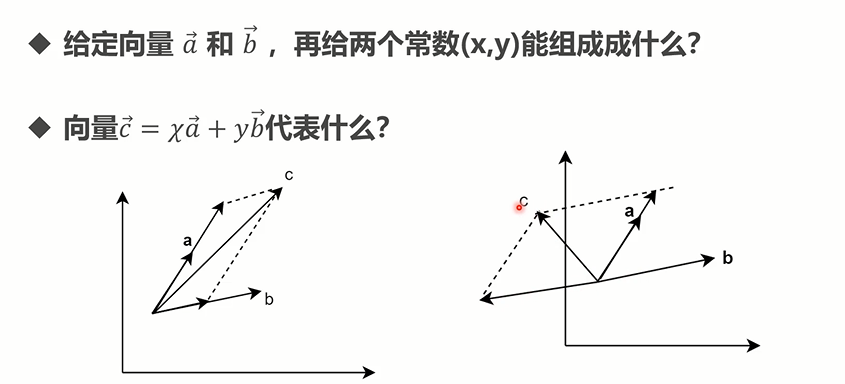
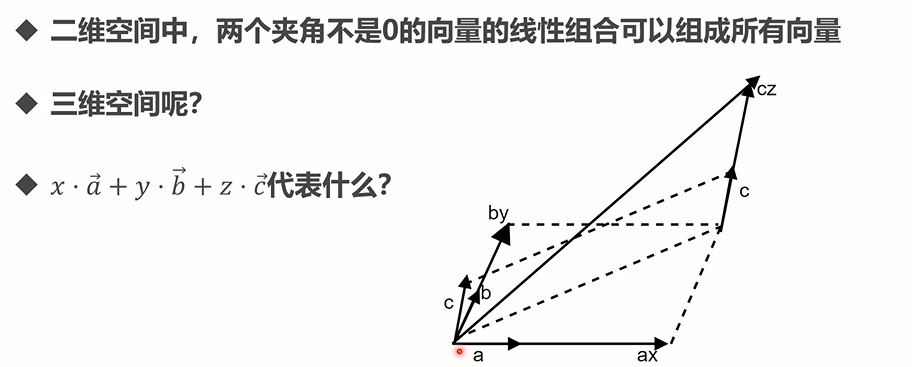
- 三维
可以组合三维中任意向量
# 向量的叉乘

向量积也叫叉积,外积,它也是向量与向量的乘积,不过需要注意的是,它的结果是个向量。它的几何意义是所得的向量与被乘向量所在平面垂直,方向由右手定则规定,大小是两个被乘向量张成的平行四边形的面积。
向量积可以被定义为:
模长:(在这里 θ 表示两向量之间的夹角(共起点的前提下)(0°≤θ≤180°),它位于这两个矢量所定义的平面上。)
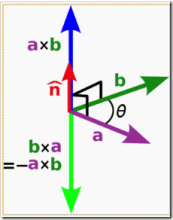
 方向:a 向量与 b 向量的向量积的方向与这两个向量所在平面垂直,且遵守右手定则。
方向:a 向量与 b 向量的向量积的方向与这两个向量所在平面垂直,且遵守右手定则。
也可以这样定义(等效):向量积 |c|=|a×b|=|a||b|sin<a,b>
即 c 的长度在数值上等于以 a,b,夹角为 θ 组成的平行四边形的面积。而 c 的方向垂直于 a 与 b 所决定的平面,c 的指向按右手定则从 a 转向 b 来确定。
计算矢量叉积是与直线和线段相关算法的核心部分。设矢量 P = (x1, y1),Q = (x2, y2),则矢量叉积定义为由(0, 0)、P1、P2 和 P1P2 所组成的平行四边形的带符号的面积, 即:P × Q = x1.y2 - y2.y1,其结果是一个标量,显然有性质 P × Q = -(Q × P) 和 P × (-Q) = -(P × Q)
向量外积的几何意义:
在三维几何中,向量 P 和向量 Q 的外积结果是一个向量,有个更通俗易懂的叫法是法向量,该向量垂直于 P 和 Q 向量构成的平面。
在 3D 图像学中,外积的概念非常有用,可以通过两个向量的外积,生成第三个垂直于 P,Q 的法向量,从而构建 X、Y、Z 坐标系。
在二维空间中,外积还有另外一个几何意义就是:|a×b| 在数值上等于由向量 P 和向量 Q 构成的平行四边形的面积。
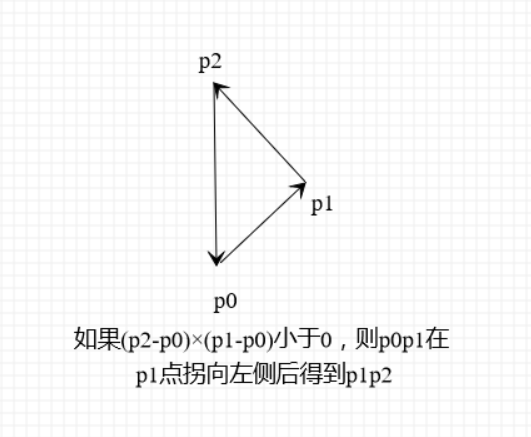
# 2d 叉乘符号的含义
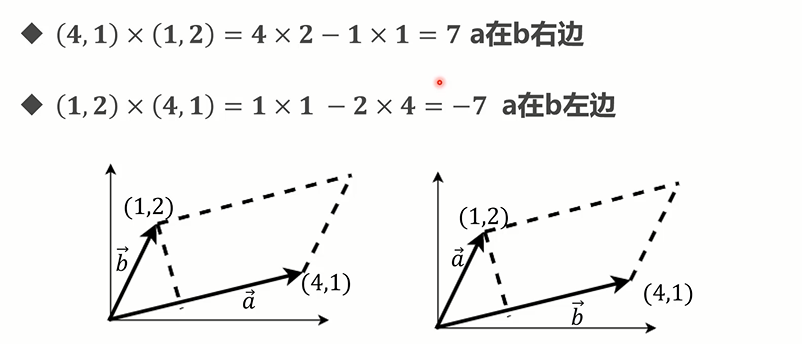
# 3d 向量叉乘
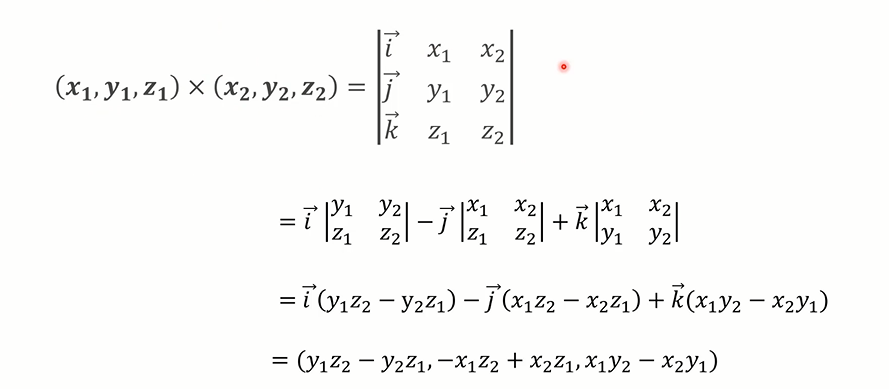
# 3D 叉乘的意义
- 向量叉乘指向向量 a 和 b 的垂直方向
- 值等于 a 和 b 形成的平行四边形面积
- a、b 和 c 的叉乘是 a、b、c 形成的平行六面体体积
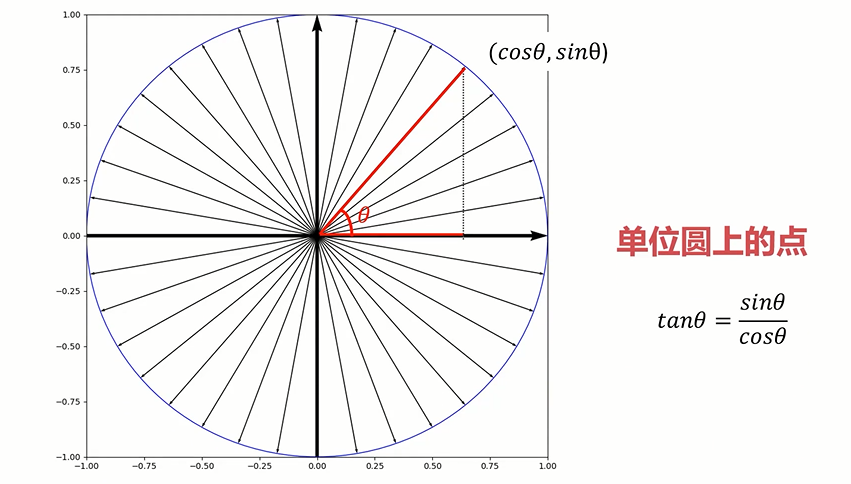
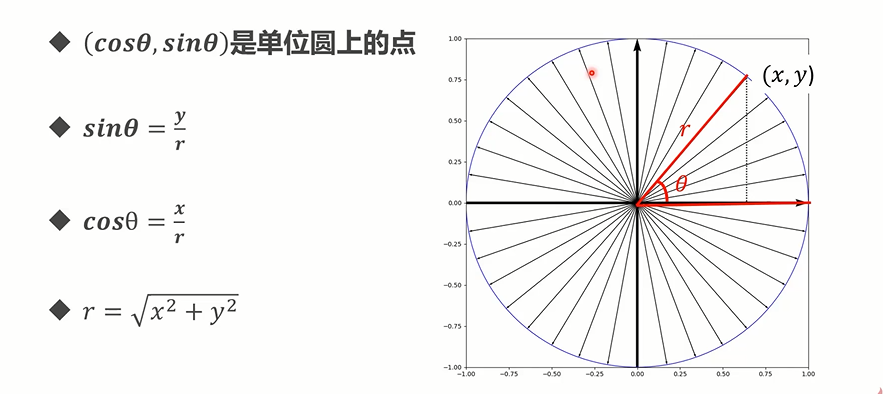
# 单位圆
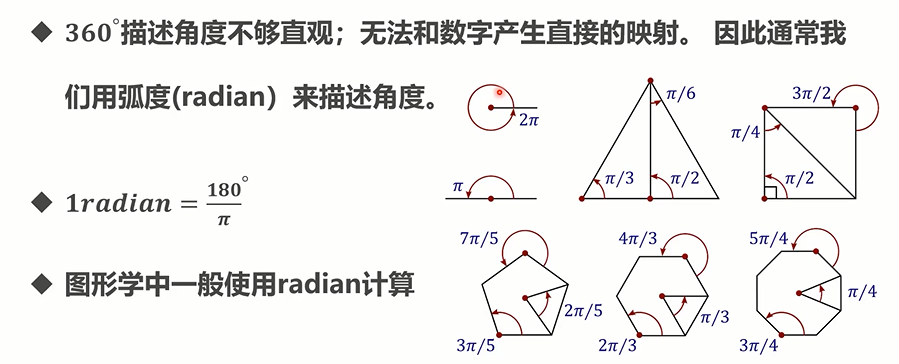
# 弧度和角度
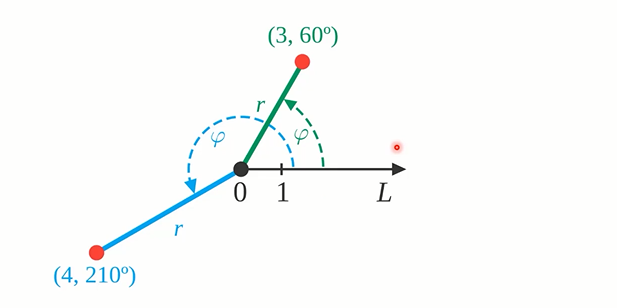
# 极坐标
由极点(pole)和射线(ray)组成的坐标系。用(角度,射线长度)描述一个点
比如图中的(3, 60°)表示射线长3,从 0L 转动 60 度。
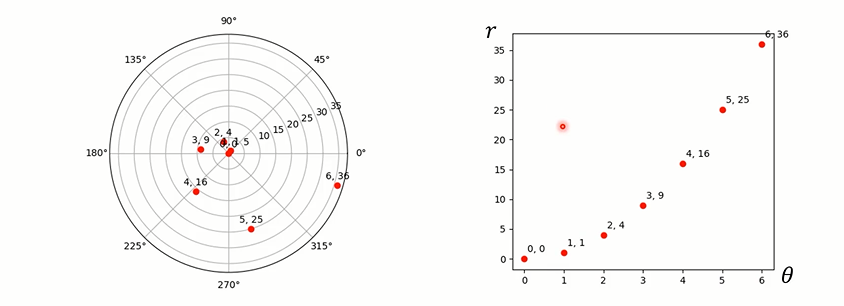
# 极坐标系
由极点和射线构成极坐标系中点:
# 三角函数的性质
# 旋转
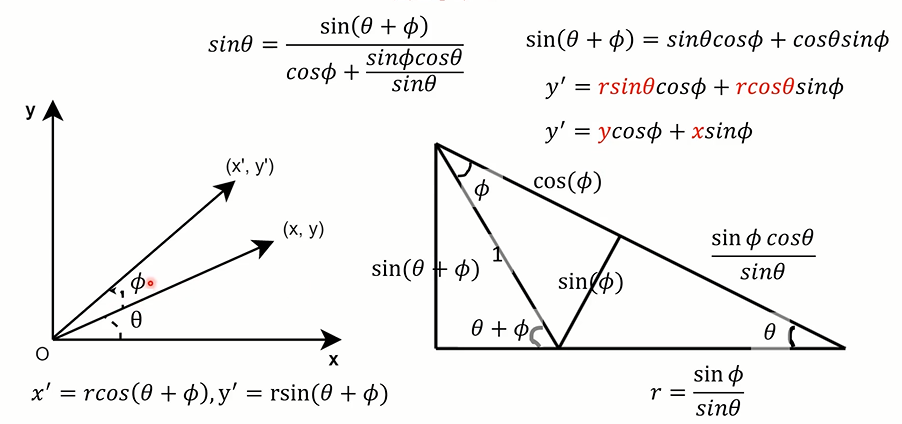
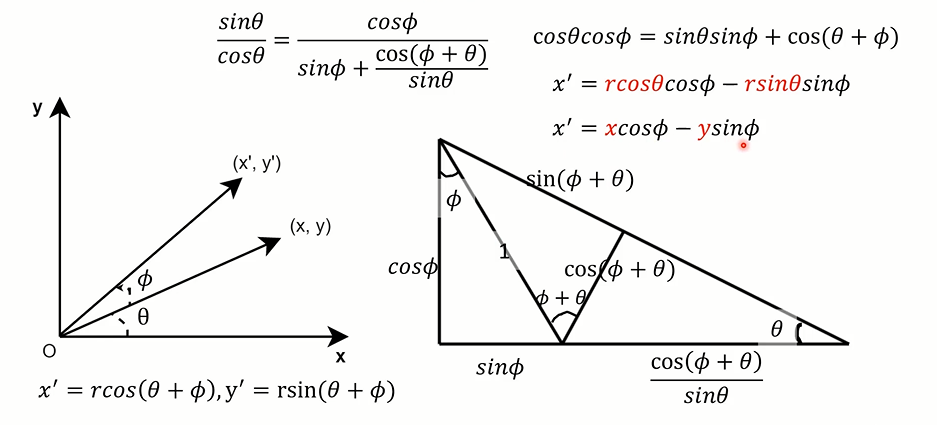
三角函数运算
- cos(a + b) = cc - ss
- sin(a + b) = cs + sc
# 矩阵
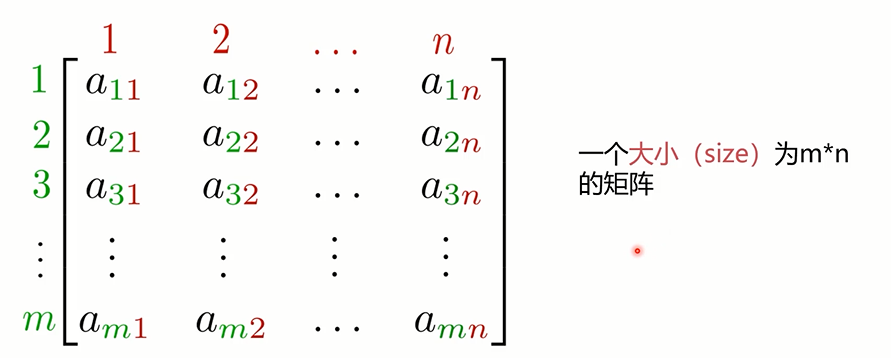
# 加减法
- 具有相同 size 的矩阵可以做加减法运算

# 乘以常数
- 矩阵可以乘以常数得到一个新的矩阵
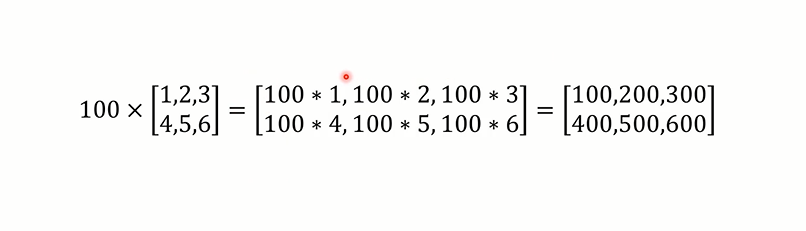
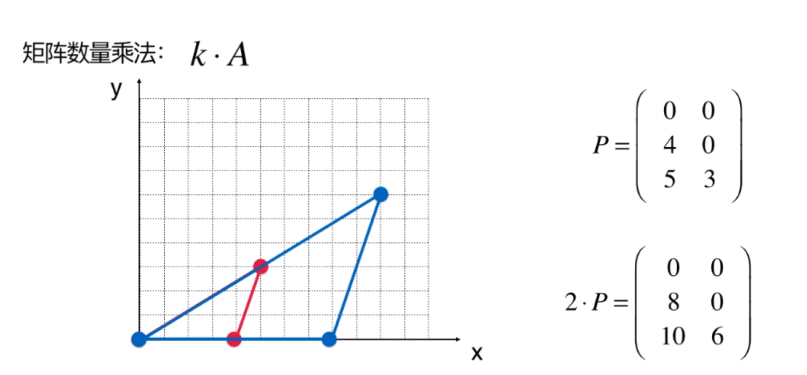
几何意义就是缩放矩阵:
# 矩阵的基本运算性质

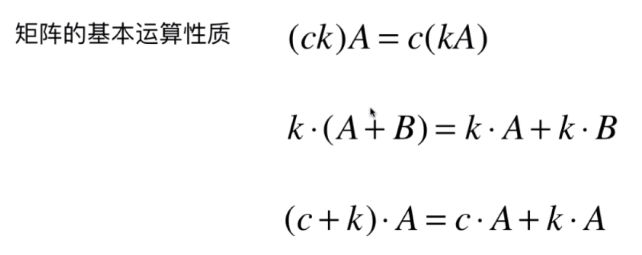
# 矩阵的转置
行列交换
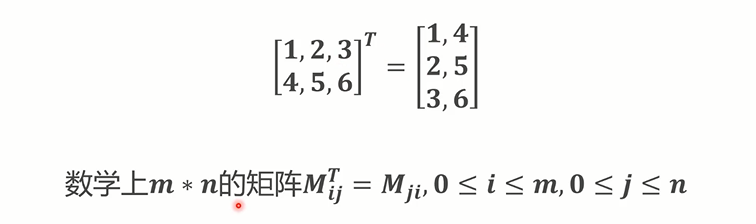
矩阵转置的性质
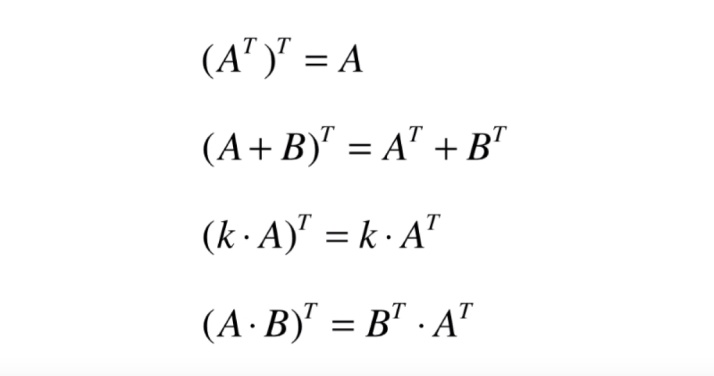
# 矩阵相乘
- AB != BA
- A(B + C) = AB + AC
- (B + C)D = BD + CD
- (AB)C = A(BC)


# 矩阵在图形变换中的应用
可以将矩阵理解为向量的函数:通过乘以一个向量会得到一个处理过后的向量;
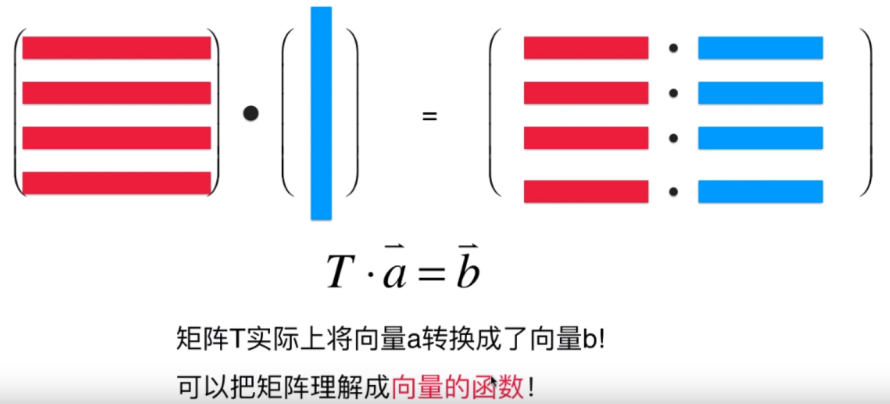
将向量横坐标以及纵坐标进行变化
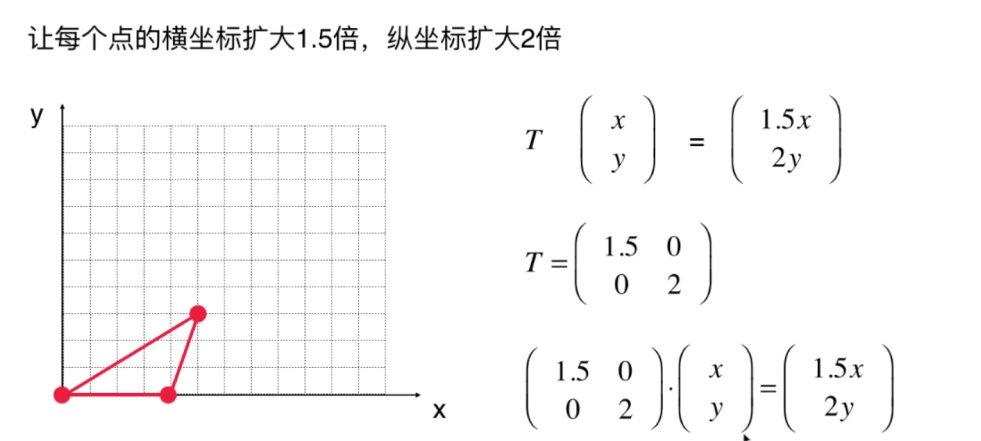

- 让每个点关于 x 轴旋转


- 让每个点关于 y 轴旋转

- 让每个点关于原点翻转

- 沿 x 方向错切
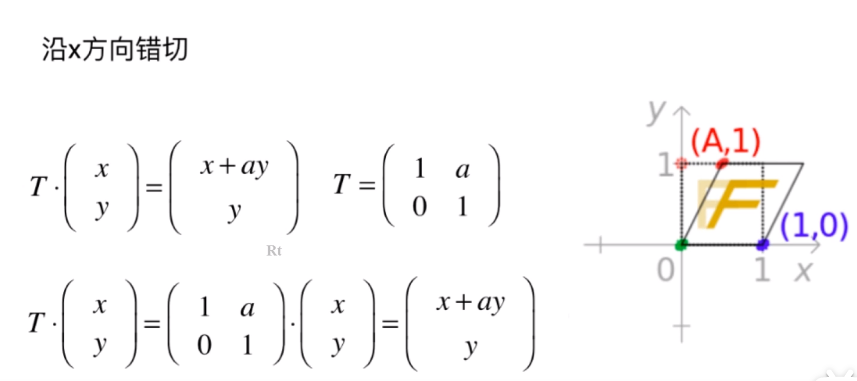
- 沿 y 方向错切
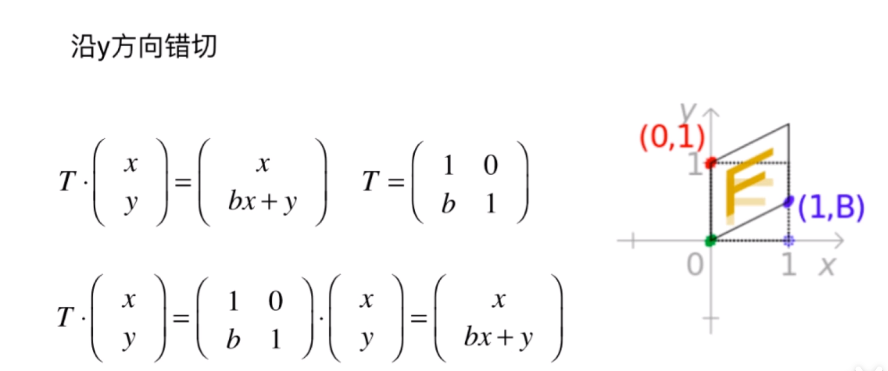
# 矩阵变换和矩阵在图形学中的应用
- 旋转矩阵推导
- 旋转一定的角度;我们设该向量的模为 d,旋转了 θ 角度,向量(x,y)与 x 轴的夹角为 α;根据三角函数我们可以得到下面等式;
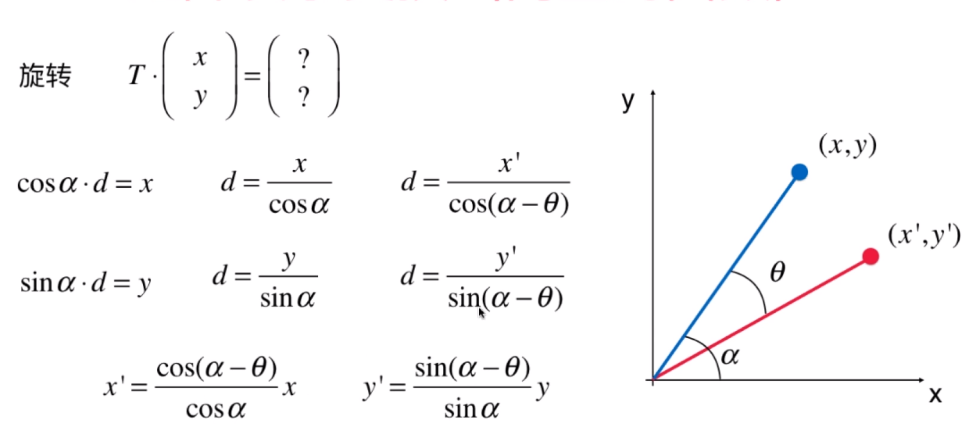
- 将三角函数展开,最后一个 sin α / cos α 是等于 tan α;tan α 是等于 y / x 的;所以最终得到下面结果:
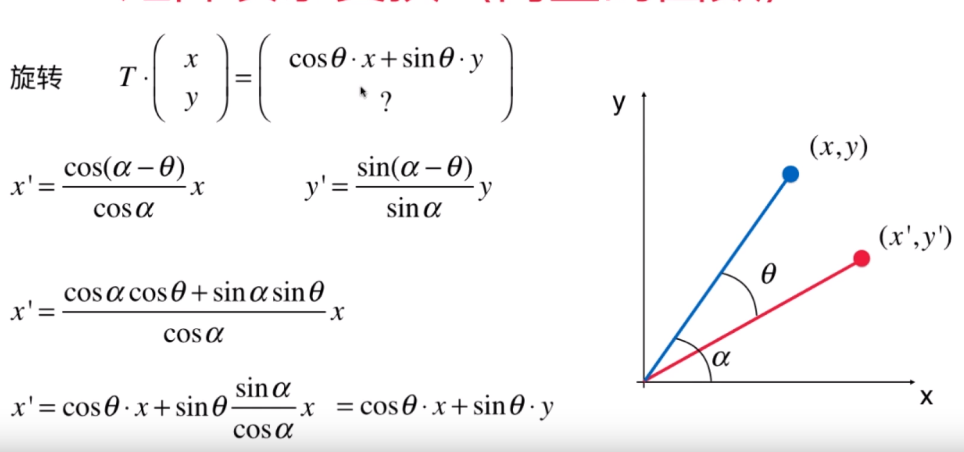
- 同理 y' 结果如下:
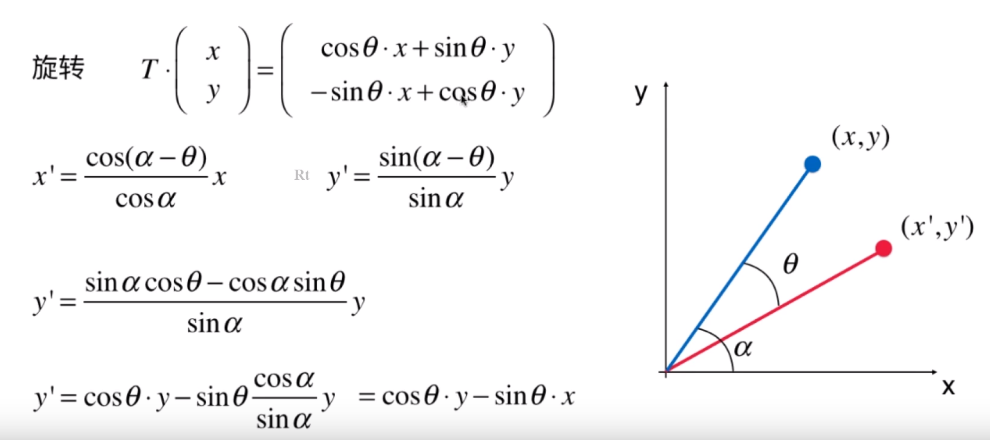
- 最终得到旋转矩阵
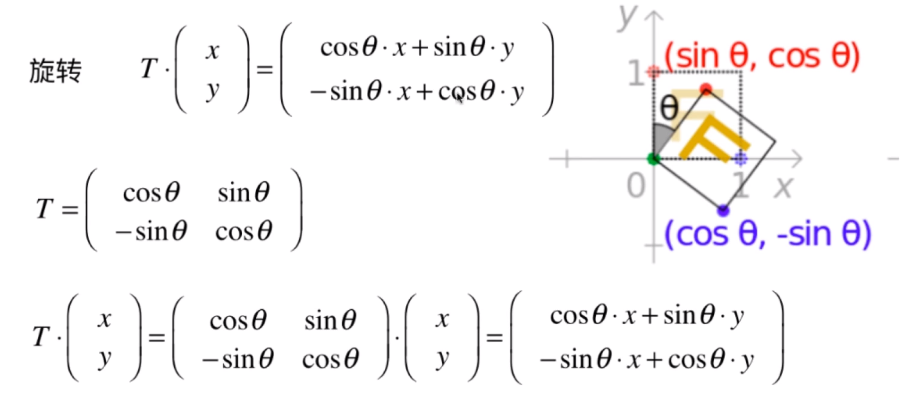
# 矩阵相乘的意义
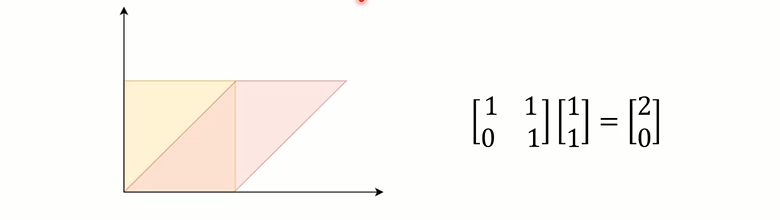
- 矩阵乘法揭示了线性变化的本质
- 点 P 和矩阵 M 的乘积 P × M 是点 P 的一种线性变换。
# 单位矩阵
- 单位矩阵乘以任何矩阵都等于该矩阵


单位矩阵的性质
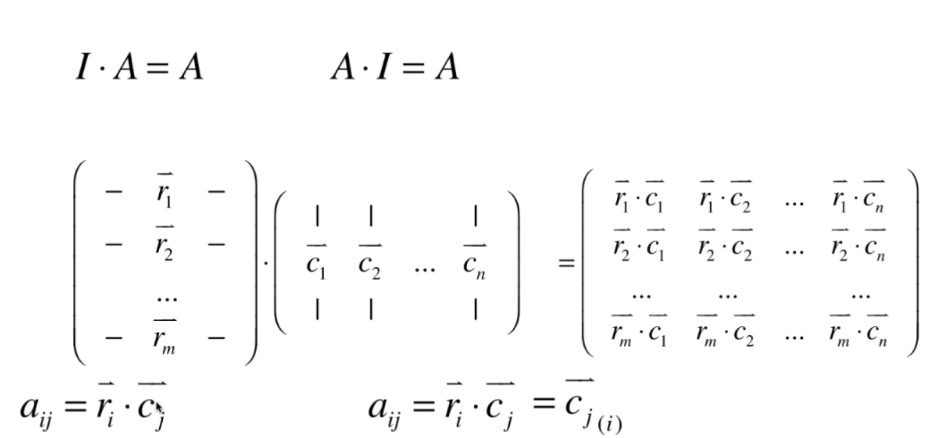
# 矩阵的逆
- A × B = B × A = 单位矩阵


- 矩阵的逆相关性质:

对于矩阵 A,如果存在逆矩阵 B,则 B 是唯一的;
A 的逆矩阵的逆矩阵是 A
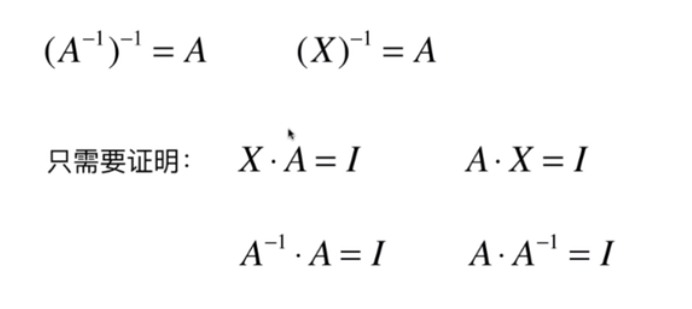
- (AB) 的逆矩阵等于 B 的逆矩阵乘以 A 的逆矩阵
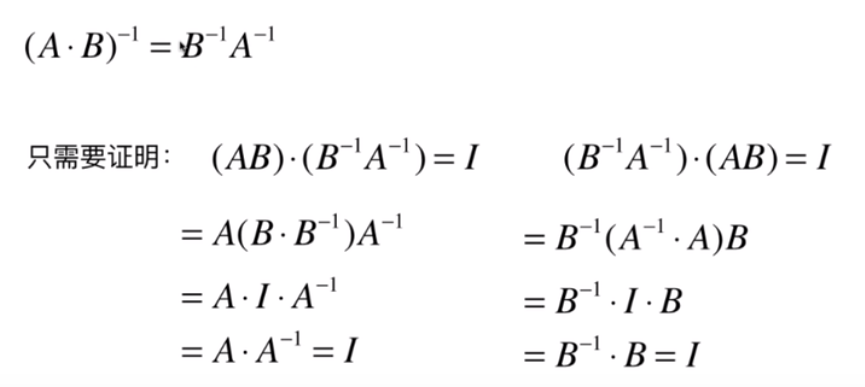
- 矩阵的转置以及逆矩阵的性质
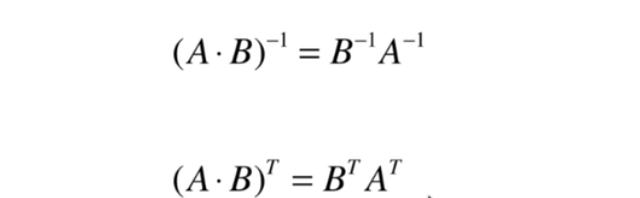
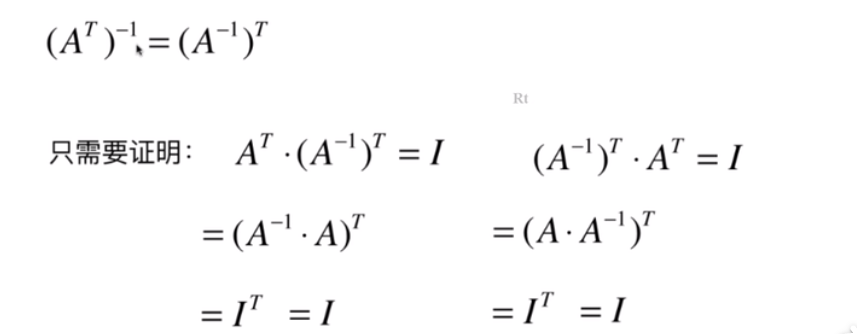
# 看待矩阵的关键视角
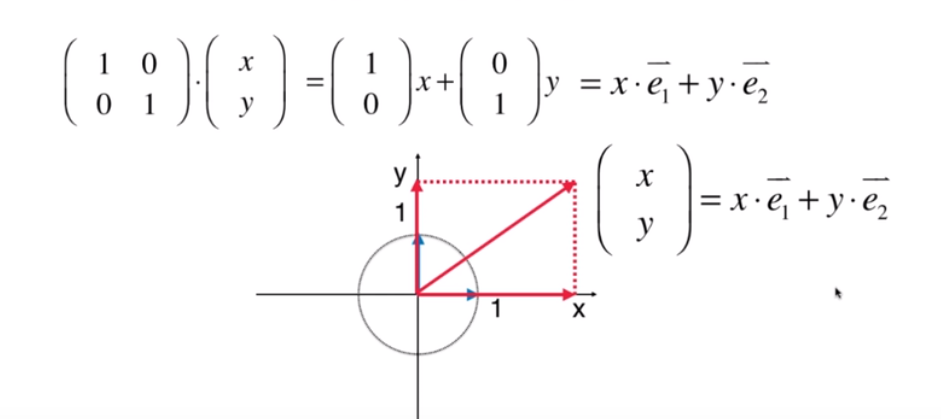
其实矩阵就是表达一个空间,比如下面的单位矩阵,我们从列的视角去看,就是表达一个 x 轴跟 y 轴的这样一个空间,然后乘以 (x, y) 向量,就是说,在 x 轴偏移了 x 倍,在 y 轴偏移了 y 倍;这样得到两个在 x 轴以及 y 轴的两个向量,然后相加就是最后的结果向量:
比如下面例子:
我们将矩阵从列视角看待,(4, 1) 和 (2, 3) 分别看做两个向量,u 跟 v,然后乘以向量 (2, 2) 就是,u、v 每个向量乘以 2;也就是将 u、v 向量扩大了 2 倍,然后两个向量相加,就是最后矩阵乘以向量的结果。
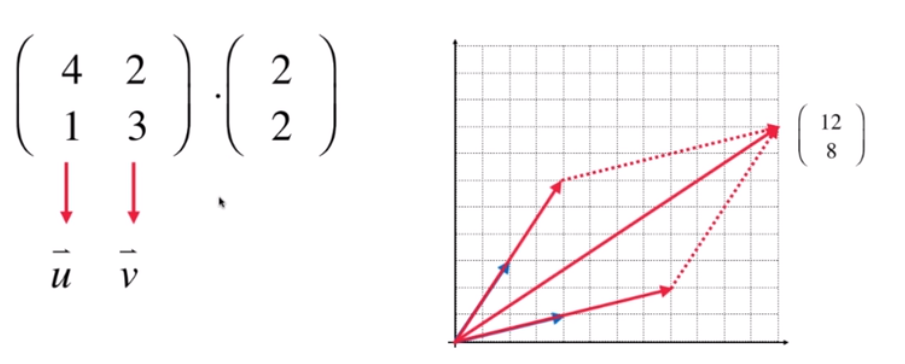
也就是说矩阵乘以向量就是将向量放在一个新的空间中,就是矩阵的列组成的向量的新空间。然后查看该向量在新空间中的位置;
上面的例子我们画出他的新空间,也就是绘制他的平行线:
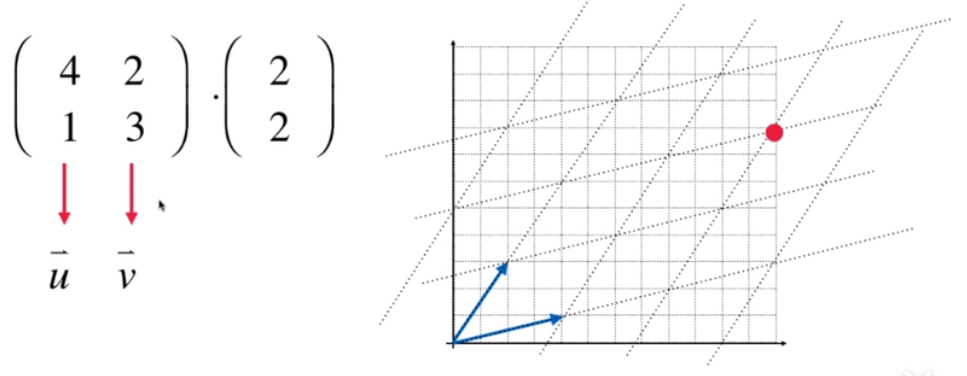
# 求矩阵的逆

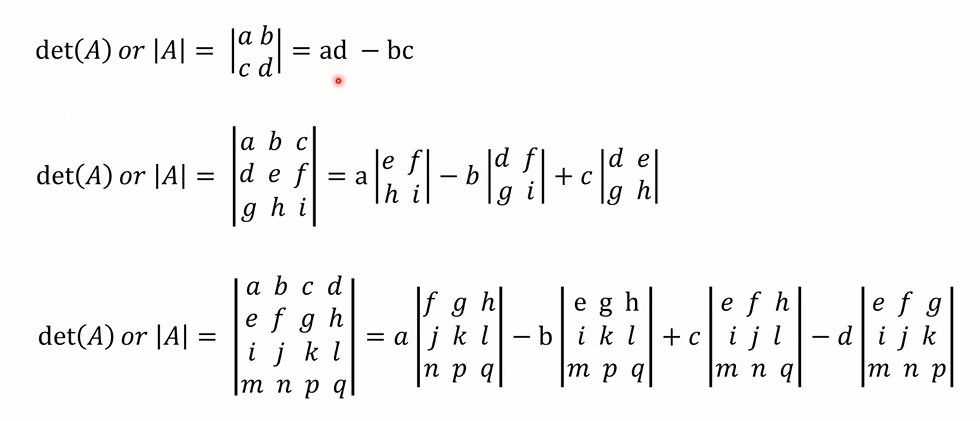
# 伴随矩阵

# 向量叉乘的行列式表示