# 光照原理
在物体表面根据光照着色,需要考虑两件事:
- 发出光线的光源的类型
- 物体表面如何反射光线
# 光源类型
真实世界中的光主要有两种类型:平行光和点光源。此外还有环境光来模拟真实世界中的非直射光(也是就是由光源发出后经过墙壁或其他物体反射后的光)
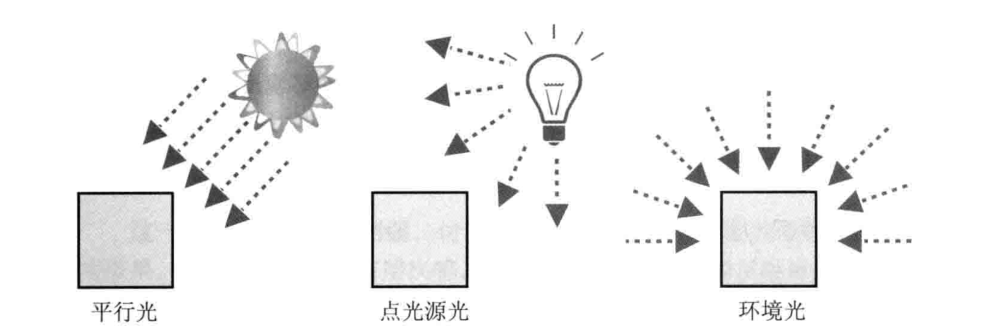
- 平行光:太阳光就是平行光,可以用一个方向和颜色来定义。
- 点光源:类似灯泡,可以用光源的位置和颜色来定义。
- 环境光:环境光从各个角度照射物体,其强度都是一致的。只需要指定颜色即可。
# 反射类型
物体反射光的位置,反射光的颜色取决于两个因素:入射光和物体表面的类型;入射光的信息包括入射光的颜色和方向,物体表面的信息包括表面的固有颜色(也称基底色)和反射特性。
物体表面反射光线的方式有:漫反射和环境反射。
# 漫反射
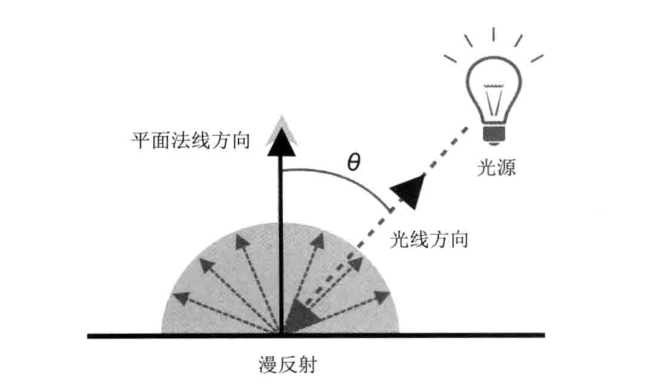
粗糙的物体表面向各个方向等强度低反射光,这种等同度地散射现象称为光的漫反射(Diffuse Reflection) 漫反射模型和视点无关于,与入射光、入射点、物体材质相关。漫反射的反射光在各个方向上是均匀的。
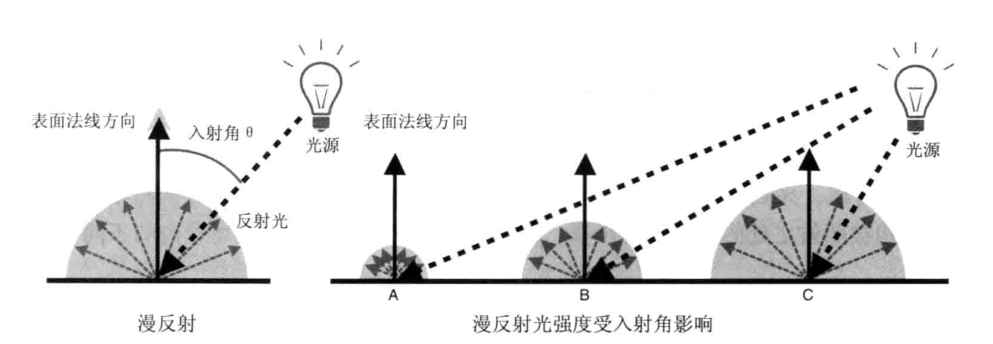
漫反射中,反射光的颜色取决于入射光的颜色、表面的基底色、入射光与表面形成的入射角。我们将入射角定义为入射光与表面的法线形成的夹角,用 θ 表示,那么漫反射光的颜色可以根据下式得到:
漫反射光颜色 = 入射光颜色 × 表面基底色 × cos θ
式子中,入射光颜色指的是点光源或平行光的颜色,乘法操作是在颜色矢量上逐分量(R、G、B)进行的。因为漫反射光在各个方向上都是均匀的,所以从任何角度看上去其强度都相等。
# 环境反射
环境反射是针对环境光而言的。在环境反射中,反射光的方向可以认为就是入射光的反方向。由于环境光照射物体的方式就是各方向均匀、强度相等的,所以反射光也是各向均匀的。可以用下面式子表述:
- 环境反射光 = 入射光颜色(环境光的颜色) × 表面基底色
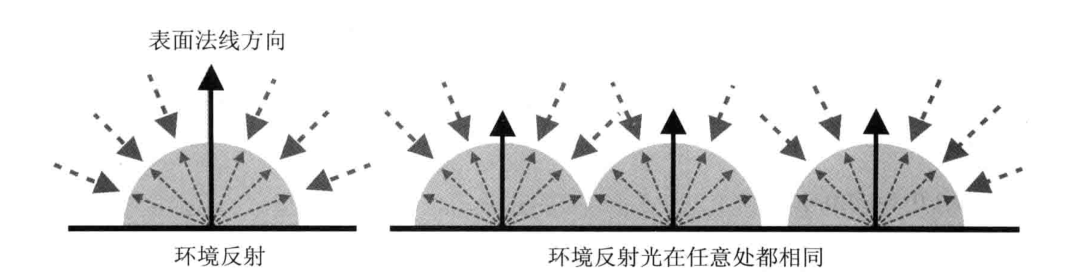
当漫反射和环境反射同时存在时,将两者加起来,就会得到物体最终被观察到的颜色:
- 表面的反射光颜色 = 漫反射光颜色 + 环境反射光颜色
# 平行光下的漫反射
我们可以根据光线方向和法线方向(物体表面的方向),来计算反射光的夹角,根据矢量的点乘。
- cos θ = 光线方向 . 法线方向
所以漫反射光的颜色可以通过下面的式子计算:
- 漫反射光颜色 = 入射光颜色 × 表面基底色 × (光线方向 . 法线方向)
这里需要注意,光线方向矢量和表面法线矢量的长度必须为 1,否则反射光的颜色就会过暗或过亮。比如矢量 n 为(nx, ny, nz)则其长度为 (nx^2 + ny ^2 + nz ^2 )^1/2。将一个矢量的长度调整为 1,同时保持方向不变的过程称为归一化。GLSL ES 提供了内置的归一化函数。还有就是这里所谓的光线方向,实际上是入射方向的的反方向。即从入射点指向光源方向(因为这样,该方向与法线方向的夹角才是入射角);
归一化:对矢量 n 进行归一化的结果是 (nx / m, ny / m, nz / m),式中 m 为 n 的长度。比如矢量 (2.0, 2.0, 1.0) 的长度为 |n| = sqrt(9) = 3,那么归一化之后就是 (2.0 / 3, 2.0 / 3, 1.0 / 3)
# 法线:表面的朝向
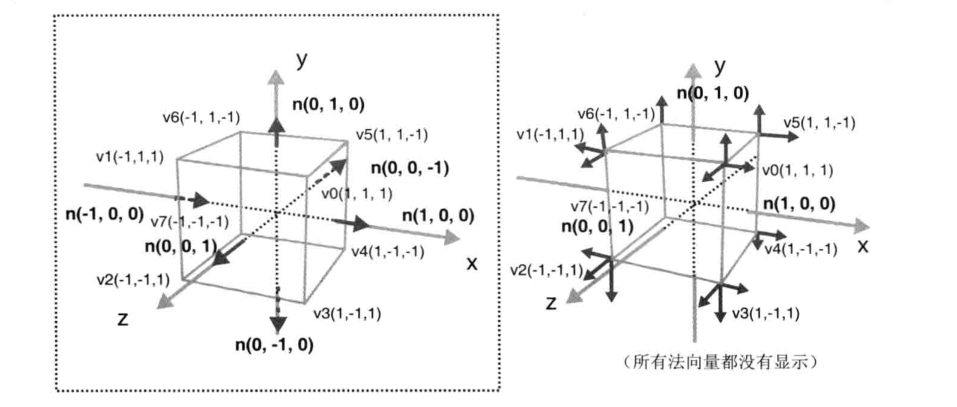
物体表面的朝向,即垂直于表面的方向,又称法线或法向量。法向量有三个分量,向量(nx, ny, nz)表示从原点(0, 0, 0)指向点(nx, ny, nz)的方向。比如说,向量 (1, 0, 0) 表示 x 轴正方向,向量 (0, 0, 1) 表示 z 轴正方向。涉及到表面和法向量的问题时,必须考虑下面两点:
- 一个表面具有两个法向量
每个表面都具有正反面,每个面各自具有一个法向量。
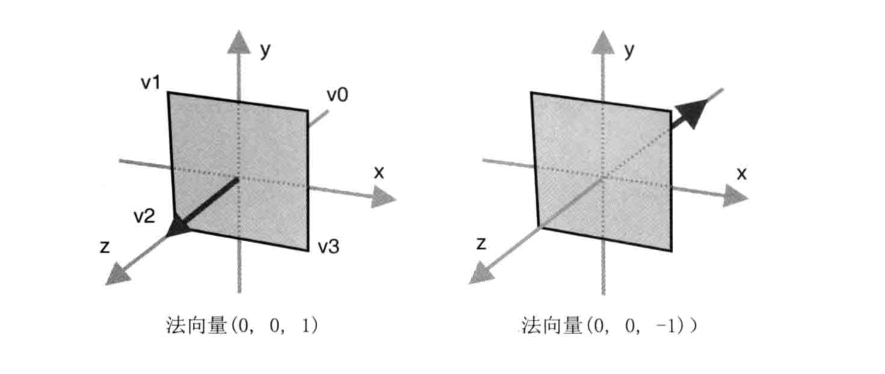
在三维图形学中,表面的正面和背面取决于绘制表面时的顶点顺序,当你按照 v0, v1, v2, v3 的顶点顺序绘制了一个平面,那么当你从正面观察这个表面时,这 4 个顶点是顺时针。通过右手法则来确定旋转方向。
- 平面的法向量唯一 由于法向量表示的是方向,与位置无关,所以一个平面只有一个法向量。换句话说,平面的任意一点都具有相同的法向量。也就是说,即使有两个不同的平面,主要其朝向相同(平行),法向量也相同。
# 漫反射模型
lld = k * la + K * ll * Cosa k 是全局光的系数,la 是全局光的光强,K 漫反射的系数,ll 代表入射光线的光强,Cosa 入射光与法线之间夹角的 cos 值。

# 示例代码
下面代码实现一个在白色平行光照射下的一个红色三角形;
// 顶点着色器
var VSHADER_SOURCE =
'attribute vec4 a_Position;\n' +
'attribute vec4 a_Color;\n' + // 表面基底色
'attribute vec4 a_Normal;\n' + // 法向量
'uniform mat4 u_MvpMatrix;\n' +
'uniform vec3 u_LightColor;\n' + // 光线颜色
'uniform vec3 u_LightDirection;\n' + // 归一化的世界坐标-光线方向
'varying vec4 v_Color;\n' +
'void main() {\n' +
' gl_Position = u_MvpMatrix * a_Position ;\n' +
// 对法向量进行归一化
' vec3 normal = normalize(a_Normal.xyz);\n' +
// 计算光线方向和法向量的点积
' float nDotL = max(dot(u_LightDirection, normal), 0.0);\n' +
// 计算反射光的颜色
' vec3 diffuse = u_LightColor * a_Color.rgb * nDotL;\n' +
' v_Color = vec4(diffuse, a_Color.a);\n' +
'}\n';
// 片元着色器
var FSHADER_SOURCE =
'#ifdef GL_ES\n' +
'precision mediump float;\n' +
'#endif\n' +
'varying vec4 v_Color;\n' +
'void main() {\n' +
' gl_FragColor = v_Color;\n' +
'}\n';
function main() {
var canvas = document.getElementById('webgl');
var gl = getWebGLContext(canvas);
if (!gl) {
console.log('Failed to get the rendering context for WebGL');
return;
}
if (!initShaders(gl, VSHADER_SOURCE, FSHADER_SOURCE)) {
console.log('Failed to intialize shaders.');
return;
}
// 设置顶点的坐标、颜色和法向量
var n = initVertexBuffers(gl);
if (n < 0) {
console.log('Failed to set the vertex information');
return;
}
gl.clearColor(0, 0, 0, 1);
gl.enable(gl.DEPTH_TEST);
var u_MvpMatrix = gl.getUniformLocation(gl.program, 'u_MvpMatrix');
var u_LightColor = gl.getUniformLocation(gl.program, 'u_LightColor');
var u_LightDirection = gl.getUniformLocation(gl.program, 'u_LightDirection');
if (!u_MvpMatrix || !u_LightColor || !u_LightDirection) {
console.log('Failed to get the storage location');
return;
}
// 设置光线颜色--白色
gl.uniform3f(u_LightColor, 1.0, 1.0, 1.0);
// 设置光线方向
var lightDirection = new Vector3([0.5, 3.0, 4.0]);
lightDirection.normalize(); // 归一化
gl.uniform3fv(u_LightDirection, lightDirection.elements);
// 计算模型矩阵以及投影矩阵
var mvpMatrix = new Matrix4();
mvpMatrix.setPerspective(30, canvas.width/canvas.height, 1, 100);
mvpMatrix.lookAt(3, 3, 7, 0, 0, 0, 0, 1, 0);
gl.uniformMatrix4fv(u_MvpMatrix, false, mvpMatrix.elements);
gl.clear(gl.COLOR_BUFFER_BIT | gl.DEPTH_BUFFER_BIT);
gl.drawElements(gl.TRIANGLES, n, gl.UNSIGNED_BYTE, 0);
}
function initVertexBuffers(gl) {
// v6----- v5
// /| /|
// v1------v0|
// | | | |
// | |v7---|-|v4
// |/ |/
// v2------v3
var vertices = new Float32Array([ // 顶点坐标
1.0, 1.0, 1.0, -1.0, 1.0, 1.0, -1.0,-1.0, 1.0, 1.0,-1.0, 1.0, // v0-v1-v2-v3 front
1.0, 1.0, 1.0, 1.0,-1.0, 1.0, 1.0,-1.0,-1.0, 1.0, 1.0,-1.0, // v0-v3-v4-v5 right
1.0, 1.0, 1.0, 1.0, 1.0,-1.0, -1.0, 1.0,-1.0, -1.0, 1.0, 1.0, // v0-v5-v6-v1 up
-1.0, 1.0, 1.0, -1.0, 1.0,-1.0, -1.0,-1.0,-1.0, -1.0,-1.0, 1.0, // v1-v6-v7-v2 left
-1.0,-1.0,-1.0, 1.0,-1.0,-1.0, 1.0,-1.0, 1.0, -1.0,-1.0, 1.0, // v7-v4-v3-v2 down
1.0,-1.0,-1.0, -1.0,-1.0,-1.0, -1.0, 1.0,-1.0, 1.0, 1.0,-1.0 // v4-v7-v6-v5 back
]);
var colors = new Float32Array([ // 颜色
1, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, // v0-v1-v2-v3 front
1, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, // v0-v3-v4-v5 right
1, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, // v0-v5-v6-v1 up
1, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, // v1-v6-v7-v2 left
1, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, // v7-v4-v3-v2 down
1, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0 // v4-v7-v6-v5 back
]);
var normals = new Float32Array([ // 法向量
0.0, 0.0, 1.0, 0.0, 0.0, 1.0, 0.0, 0.0, 1.0, 0.0, 0.0, 1.0, // v0-v1-v2-v3 front
1.0, 0.0, 0.0, 1.0, 0.0, 0.0, 1.0, 0.0, 0.0, 1.0, 0.0, 0.0, // v0-v3-v4-v5 right
0.0, 1.0, 0.0, 0.0, 1.0, 0.0, 0.0, 1.0, 0.0, 0.0, 1.0, 0.0, // v0-v5-v6-v1 up
-1.0, 0.0, 0.0, -1.0, 0.0, 0.0, -1.0, 0.0, 0.0, -1.0, 0.0, 0.0, // v1-v6-v7-v2 left
0.0,-1.0, 0.0, 0.0,-1.0, 0.0, 0.0,-1.0, 0.0, 0.0,-1.0, 0.0, // v7-v4-v3-v2 down
0.0, 0.0,-1.0, 0.0, 0.0,-1.0, 0.0, 0.0,-1.0, 0.0, 0.0,-1.0 // v4-v7-v6-v5 back
]);
// 顶点索引
var indices = new Uint8Array([
0, 1, 2, 0, 2, 3, // front
4, 5, 6, 4, 6, 7, // right
8, 9,10, 8,10,11, // up
12,13,14, 12,14,15, // left
16,17,18, 16,18,19, // down
20,21,22, 20,22,23 // back
]);
if (!initArrayBuffer(gl, 'a_Position', vertices, 3, gl.FLOAT)) return -1;
if (!initArrayBuffer(gl, 'a_Color', colors, 3, gl.FLOAT)) return -1;
if (!initArrayBuffer(gl, 'a_Normal', normals, 3, gl.FLOAT)) return -1;
var indexBuffer = gl.createBuffer();
if (!indexBuffer) {
console.log('Failed to create the buffer object');
return false;
}
gl.bindBuffer(gl.ELEMENT_ARRAY_BUFFER, indexBuffer);
gl.bufferData(gl.ELEMENT_ARRAY_BUFFER, indices, gl.STATIC_DRAW);
return indices.length;
}
function initArrayBuffer (gl, attribute, data, num, type) {
var buffer = gl.createBuffer();
if (!buffer) {
console.log('Failed to create the buffer object');
return false;
}
gl.bindBuffer(gl.ARRAY_BUFFER, buffer);
gl.bufferData(gl.ARRAY_BUFFER, data, gl.STATIC_DRAW);
var a_attribute = gl.getAttribLocation(gl.program, attribute);
if (a_attribute < 0) {
console.log('Failed to get the storage location of ' + attribute);
return false;
}
gl.vertexAttribPointer(a_attribute, num, type, false, 0, 0);
gl.enableVertexAttribArray(a_attribute);
gl.bindBuffer(gl.ARRAY_BUFFER, null);
return true;
}
a_Normal 变量是 vec4 类型的,使用前三个分量 x、y 和 z 表示法线方向,所以上面例子是将这三个分量进行归一化处理。
nDotL 是计算光线方向与法线方向的点乘,使用了内置的 max() 方法,如果点积大于 0 ,就将点积赋值给 nDotL 变量,如果小于 0,就将 0 赋给该变量。点积值小于 0,说明 θ 大于 90 °,也就是入射反方向与表面法向量的夹角,θ 大于 90 度说明光线照射在表面的背面上,如下图:

注意我们使用 a_Color 变量就是顶点的颜色,被从 vec4 对象转换成了 vec3 对象,因为其第 4 分负能量是透明度,与计算物体反射光线无关。实际上,物体表面的透明度确实会影响物体的外观。但这时光照的计算较为复杂。这里不进行计算。
# 环境光下的漫反射
上面通过平行光渲染的物体,可以看到他的背光面,几乎黑到看不见。实际上,那些背光的面试被非直射光照亮的,前面提到的环境光就起到了这部分非直射光的作用,他使得场景更加逼真。因为环境光均匀地从各个角度照在物体表面,所以由环境光反射产生的颜色只取决于光的颜色和表面的基底色。如下公式:
环境反射光颜色 = 入射光颜色 × 表面基底色
我们改进上面的例子,加上环境光所产生的反射光颜色,公式如下:
表面的反射光颜色 = 漫反射光颜色 + 环境反射光颜色
示例代码:
// 顶点着色器
var VSHADER_SOURCE =
'attribute vec4 a_Position;\n' +
'attribute vec4 a_Color;\n' +
'attribute vec4 a_Normal;\n' + // 法线
'uniform mat4 u_MvpMatrix;\n' +
'uniform vec3 u_DiffuseLight;\n' + // 漫反射光
'uniform vec3 u_LightDirection;\n' + // 漫反射光方向
'uniform vec3 u_AmbientLight;\n' + // 环境光
'varying vec4 v_Color;\n' +
'void main() {\n' +
' gl_Position = u_MvpMatrix * a_Position;\n' +
' vec3 normal = normalize(a_Normal.xyz);\n' +
' float nDotL = max(dot(u_LightDirection, normal), 0.0);\n' +
' vec3 diffuse = u_DiffuseLight * a_Color.rgb * nDotL;\n' +
// 计算环境光产生的反射光颜色
' vec3 ambient = u_AmbientLight * a_Color.rgb;\n' +
// 将以上两者相加得到物体最终的颜色
' v_Color = vec4(diffuse + ambient, a_Color.a);\n' +
'}\n';
// 片元着色器同上
function main() {
var u_AmbientLight = gl.getUniformLocation(gl.program, 'u_AmbientLight');
// 设置环境光--较微弱的白色光
gl.uniform3f(u_AmbientLight, 0.2, 0.2, 0.2);
// 其他代码同上
}
顶点着色器新增 u_AmbientLight 接收环境光的颜色值,然后与基底色 a_Color 计算产生的反射光的颜色存储在 ambient 变量中,然后与平行光产生的颜色 deffuse 进行相加,得到最终物体表面显示的颜色。
# 运动物体的光照效果
这里主要是将当物体通过模型矩阵等变化后,如何进行渲染光线,主要需要解决法线方向的变化,通过逆转置矩阵解决。
立方体旋转时,每个表面的法向量也会随之变化;如下图,我们从 z 轴负方向观察一个立方体,最左边是立方体的初始状态。图中标出了立方体右侧面的法向量(1, 0, 0),他指向 x 轴正方向,然后对该立方体进行变换,观察右侧法向量随之变化的情况:
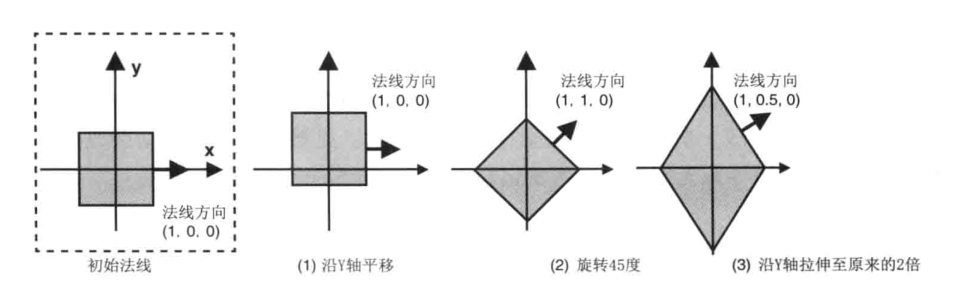
由上图可知:
- 平移变换不会改变法向量,因为平移不会改变物体的方向
- 旋转变化会改变法向量,因为旋转改变了物体的方向
- 缩放变换对法向量的影响较为复杂,最右侧的图显示了立方体先旋转了 45°,再在 y 轴上拉伸至原来的 2 倍,此时法向量改变了。因为表面的朝向改变了。但是如果缩放比例在所有的轴上都一致的话,那么法向量就不会变换,最后,即使物体在某些轴上的缩放比例并不一致,法向量也并不一定会变化,比如将最左侧图中的立方体在 y 轴放心啊跟上拉伸两倍。法向量就不会变化。
显然,在对物体进行不同变换时,法向量的变化情况较为复杂,可以通过逆转置矩阵来进行变化。
# 逆转置矩阵
我们可以使用逆转置矩阵通过与变换之前的法向量相乘。
逆矩阵的含义是:如果矩阵 M 的逆矩阵是 R,那么 R * M 或 M * R 的结果都是单位矩阵。转置的意思是,将矩阵的行列进行调换。
用法向量乘以模型矩阵的逆转置矩阵,就可以求得变换后的法向量。
封装方法:
// 使自身成为矩阵 other 的逆矩阵
Matrix4.prototype.setInverseOf = function(other) {
var i, s, d, inv, det;
s = other.elements;
d = this.elements;
inv = new Float32Array(16);
inv[0] = s[5]*s[10]*s[15] - s[5] *s[11]*s[14] - s[9] *s[6]*s[15]
+ s[9]*s[7] *s[14] + s[13]*s[6] *s[11] - s[13]*s[7]*s[10];
inv[4] = - s[4]*s[10]*s[15] + s[4] *s[11]*s[14] + s[8] *s[6]*s[15]
- s[8]*s[7] *s[14] - s[12]*s[6] *s[11] + s[12]*s[7]*s[10];
inv[8] = s[4]*s[9] *s[15] - s[4] *s[11]*s[13] - s[8] *s[5]*s[15]
+ s[8]*s[7] *s[13] + s[12]*s[5] *s[11] - s[12]*s[7]*s[9];
inv[12] = - s[4]*s[9] *s[14] + s[4] *s[10]*s[13] + s[8] *s[5]*s[14]
- s[8]*s[6] *s[13] - s[12]*s[5] *s[10] + s[12]*s[6]*s[9];
inv[1] = - s[1]*s[10]*s[15] + s[1] *s[11]*s[14] + s[9] *s[2]*s[15]
- s[9]*s[3] *s[14] - s[13]*s[2] *s[11] + s[13]*s[3]*s[10];
inv[5] = s[0]*s[10]*s[15] - s[0] *s[11]*s[14] - s[8] *s[2]*s[15]
+ s[8]*s[3] *s[14] + s[12]*s[2] *s[11] - s[12]*s[3]*s[10];
inv[9] = - s[0]*s[9] *s[15] + s[0] *s[11]*s[13] + s[8] *s[1]*s[15]
- s[8]*s[3] *s[13] - s[12]*s[1] *s[11] + s[12]*s[3]*s[9];
inv[13] = s[0]*s[9] *s[14] - s[0] *s[10]*s[13] - s[8] *s[1]*s[14]
+ s[8]*s[2] *s[13] + s[12]*s[1] *s[10] - s[12]*s[2]*s[9];
inv[2] = s[1]*s[6]*s[15] - s[1] *s[7]*s[14] - s[5] *s[2]*s[15]
+ s[5]*s[3]*s[14] + s[13]*s[2]*s[7] - s[13]*s[3]*s[6];
inv[6] = - s[0]*s[6]*s[15] + s[0] *s[7]*s[14] + s[4] *s[2]*s[15]
- s[4]*s[3]*s[14] - s[12]*s[2]*s[7] + s[12]*s[3]*s[6];
inv[10] = s[0]*s[5]*s[15] - s[0] *s[7]*s[13] - s[4] *s[1]*s[15]
+ s[4]*s[3]*s[13] + s[12]*s[1]*s[7] - s[12]*s[3]*s[5];
inv[14] = - s[0]*s[5]*s[14] + s[0] *s[6]*s[13] + s[4] *s[1]*s[14]
- s[4]*s[2]*s[13] - s[12]*s[1]*s[6] + s[12]*s[2]*s[5];
inv[3] = - s[1]*s[6]*s[11] + s[1]*s[7]*s[10] + s[5]*s[2]*s[11]
- s[5]*s[3]*s[10] - s[9]*s[2]*s[7] + s[9]*s[3]*s[6];
inv[7] = s[0]*s[6]*s[11] - s[0]*s[7]*s[10] - s[4]*s[2]*s[11]
+ s[4]*s[3]*s[10] + s[8]*s[2]*s[7] - s[8]*s[3]*s[6];
inv[11] = - s[0]*s[5]*s[11] + s[0]*s[7]*s[9] + s[4]*s[1]*s[11]
- s[4]*s[3]*s[9] - s[8]*s[1]*s[7] + s[8]*s[3]*s[5];
inv[15] = s[0]*s[5]*s[10] - s[0]*s[6]*s[9] - s[4]*s[1]*s[10]
+ s[4]*s[2]*s[9] + s[8]*s[1]*s[6] - s[8]*s[2]*s[5];
det = s[0]*inv[0] + s[1]*inv[4] + s[2]*inv[8] + s[3]*inv[12];
if (det === 0) {
return this;
}
det = 1 / det;
for (i = 0; i < 16; i++) {
d[i] = inv[i] * det;
}
return this;
};
// 将自身进行转置操作,并将自身设为转置后的结果
Matrix4.prototype.transpose = function() {
var e, t;
e = this.elements;
t = e[ 1]; e[ 1] = e[ 4]; e[ 4] = t;
t = e[ 2]; e[ 2] = e[ 8]; e[ 8] = t;
t = e[ 3]; e[ 3] = e[12]; e[12] = t;
t = e[ 6]; e[ 6] = e[ 9]; e[ 9] = t;
t = e[ 7]; e[ 7] = e[13]; e[13] = t;
t = e[11]; e[11] = e[14]; e[14] = t;
return this;
};
使用如下代码:
Matrix4 normalMatrix = new Matrix4()
// 根据模型矩阵计算用来变换法向量的矩阵
normalMatrix.setInverseOf(modelMatrix)
normalMatrix.transpose()
# 示例程序
下面代码展示了将立方体绕 z 轴顺时针旋转 90 °,然后沿 y 轴平移 0.9 个单位,并且处于平行光和环境光的照射下。
// LightedTranslatedRotatedCube.js (c) 2012 matsuda
// Vertex shader program
var VSHADER_SOURCE =
'attribute vec4 a_Position;\n' +
'attribute vec4 a_Color;\n' +
'attribute vec4 a_Normal;\n' +
'uniform mat4 u_MvpMatrix;\n' +
'uniform mat4 u_NormalMatrix;\n' + // 用来变换法向量的矩阵
'uniform vec3 u_LightColor;\n' + // 光的颜色
'uniform vec3 u_LightDirection;\n' + // 归一化的世界坐标
'uniform vec3 u_AmbientLight;\n' + // 环境光颜色
'varying vec4 v_Color;\n' +
'void main() {\n' +
' gl_Position = u_MvpMatrix * a_Position;\n' +
// 计算变换后的法向量并归一化
' vec3 normal = normalize(vec3(u_NormalMatrix * a_Normal));\n' +
// 计算光线和法向量的点击
' float nDotL = max(dot(u_LightDirection, normal), 0.0);\n' +
// 计算漫反射光的颜色
' vec3 diffuse = u_LightColor * a_Color.rgb * nDotL;\n' +
// 计算环境光产生的反射光的颜色
' vec3 ambient = u_AmbientLight * a_Color.rgb;\n' +
// 将以上两者相加作为最终的颜色
' v_Color = vec4(diffuse + ambient, a_Color.a);\n' +
'}\n';
// 片元着色器同上
function main() {
var u_NormalMatrix = gl.getUniformLocation(gl.program, 'u_NormalMatrix');
var normalMatrix = new Matrix4(); // 用来变换法向量的矩阵
// 根据模型矩阵计算用来变化法向量的矩阵
normalMatrix.setInverseOf(modelMatrix);
normalMatrix.transpose();
gl.uniformMatrix4fv(u_NormalMatrix, false, normalMatrix.elements);
}
# 点光源
点光源与平行光是不同的,在对点光源下的物体进行着色时,需要在每个入射点计算点光源在该处的方向。
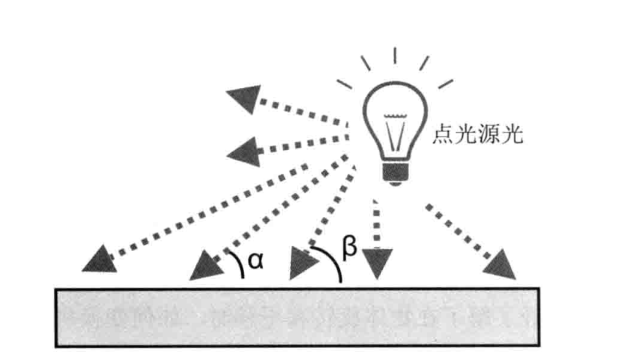
前面通过每个顶点的法向量和平行光入射方向来计算反射光的颜色。点光源的计算也是这种方法,只不过点光源的方向不再是恒定不变的,而要根据每个顶点的位置逐一计算。着色器需要知道点光源自身所在位置,而不是光的方向。
漫反射光颜色 = 入射光颜色 × 表面基底色 × cosθ 漫反射光颜色 = 入射光颜色 × 表面基底色 × (光线方向 . 法线方向)
# 示例代码
使用点光源下渲染一个红色立方体:
// 顶点着色器
var VSHADER_SOURCE =
'attribute vec4 a_Position;\n' +
'attribute vec4 a_Color;\n' +
'attribute vec4 a_Normal;\n' +
'uniform mat4 u_MvpMatrix;\n' +
'uniform mat4 u_ModelMatrix;\n' + // 模型矩阵
'uniform mat4 u_NormalMatrix;\n' + // 用来变换法向量的矩阵
'uniform vec3 u_LightColor;\n' + // 光的颜色
'uniform vec3 u_LightPosition;\n' + // 光源位置
'uniform vec3 u_AmbientLight;\n' + // 环境光的颜色
'varying vec4 v_Color;\n' +
'void main() {\n' +
' gl_Position = u_MvpMatrix * a_Position;\n' +
// 计算变换后的法向量归一化
' vec3 normal = normalize(vec3(u_NormalMatrix * a_Normal));\n' +
// 计算顶点的世界坐标
' vec4 vertexPosition = u_ModelMatrix * a_Position;\n' +
// 计算光线方向并归一化
' vec3 lightDirection = normalize(u_LightPosition - vec3(vertexPosition));\n' +
// 计算光线方向和法向量的点积
' float nDotL = max(dot(lightDirection, normal), 0.0);\n' +
// 计算漫反射光的颜色
' vec3 diffuse = u_LightColor * a_Color.rgb * nDotL;\n' +
// 计算环境光产生的反射光的颜色
' vec3 ambient = u_AmbientLight * a_Color.rgb;\n' +
// 将以上两者相加作为最终的颜色
' v_Color = vec4(diffuse + ambient, a_Color.a);\n' +
'}\n';
// 片元着色器同上
// 这里只写一些关键代码
function main() {
var u_LightPosition = gl.getUniformLocation(gl.program, 'u_LightPosition');
// 设置光源位置
gl.uniform3f(u_LightPosition, 2.3, 4.0, 3.5);
}
这里的代码只是增加了传入点光源的位置,最关键的代码是在顶点着色器中。首先使用模型矩阵变换顶点坐标,获得顶点在世界坐标系中的坐标(即变换后的坐标),以便计算点光源在顶点处的方向。这里的光线方向需要根据点光源坐标减去顶点坐标得到的矢量。这里需要注意的是,还是需要将计算出的光线方向矢量进行归一化,以保证光线方向矢量的长度为 1.0(是因为向量叉乘来计算 cos θ,所以保证向量的模为 1)最后,计算光线方向矢量与法向量的点积,从而算出每个顶点的颜色。

上面是渲染的结果,但是我们会法线立方体表面上会有一些不自然的线条。出现该现象的原因是因为我们之前说过颜色的内插引起的,webgl 系统会根据顶点的颜色,内插出表面上每个片元的颜色。实际上,点光源照射到一个表面上,所产生的效果(即每个片元获得的颜色)与简单实用 4 个顶点颜色(虽然这 4 个 顶点的颜色也是由点光源产生的)内插出的效果并不完全相同。如果是球体,差异会很大,如下图:
下图没有通过逐片元计算光照,
 下图通过逐片元计算光照
下图通过逐片元计算光照

所以为了使效果更加逼真,我们需要对表面的每一点(而不仅仅是 4 个顶点)计算光照效果。
# 逐片元光照
我们并不是在表面的每一个点上计算光照产生的颜色,我们只需要逐片元地进行计算。
如下代码:
// 顶点着色器
var VSHADER_SOURCE =
'attribute vec4 a_Position;\n' +
'attribute vec4 a_Color;\n' +
'attribute vec4 a_Normal;\n' +
'uniform mat4 u_MvpMatrix;\n' +
'uniform mat4 u_ModelMatrix;\n' + // 模型矩阵
'uniform mat4 u_NormalMatrix;\n' + // 用来变换法向量的矩阵
'varying vec4 v_Color;\n' +
'varying vec3 v_Normal;\n' +
'varying vec3 v_Position;\n' +
'void main() {\n' +
' gl_Position = u_MvpMatrix * a_Position;\n' +
// 计算顶点的世界坐标
' v_Position = vec3(u_ModelMatrix * a_Position);\n' +
' v_Normal = normalize(vec3(u_NormalMatrix * a_Normal));\n' +
' v_Color = a_Color;\n' +
'}\n';
// 片元着色器
var FSHADER_SOURCE =
'#ifdef GL_ES\n' +
'precision mediump float;\n' +
'#endif\n' +
'uniform vec3 u_LightColor;\n' + // 光的颜色
'uniform vec3 u_LightPosition;\n' + // 光源位置
'uniform vec3 u_AmbientLight;\n' + // 环境光颜色
'varying vec3 v_Normal;\n' +
'varying vec3 v_Position;\n' +
'varying vec4 v_Color;\n' +
'void main() {\n' +
// 对法线进行归一化,因为其内插之后长度不一定是 1.0
' vec3 normal = normalize(v_Normal);\n' +
// 计算光线方向并归一化
' vec3 lightDirection = normalize(u_LightPosition - v_Position);\n' +
// 计算光线方向与法向量点击
' float nDotL = max(dot(lightDirection, normal), 0.0);\n' +
// 计算反射光与环境光的颜色
' vec3 diffuse = u_LightColor * v_Color.rgb * nDotL;\n' +
' vec3 ambient = u_AmbientLight * v_Color.rgb;\n' +
' gl_FragColor = vec4(diffuse + ambient, v_Color.a);\n' +
'}\n';
// js 代码同上程序
为了逐片元地计算光照,主要知道:
- 片元在世界坐标系下的坐标
- 片元处表面的法向量。可以在顶点着色器中,将顶点的世界坐标和法向量以 varying 变量的形式传入片元着色器,片元着色器中的同名变量就已经是内插后的逐片元值了。
注意上面代码在片元着色器中获取到的 v_Position 是通过内插得到了片元的世界坐标。类似的 v_Normal 也是经过内插得到的逐片元的 v_Normal 变量,也就是片元的法向量。
片元着色器计算光照与之前的程序一样,首先对法向量 v_Normal 进行归一化处理,因为内插之后法向量可能不再是 1.0 了,然后,计算片元处的光线方向并对其归一化。接着计算法向量与光线方向的点积。最后分别计算点光源和环境光产生的反射光颜色。最终计算片元的颜色。
如果场景中有超过一个点光源,那么就需要在片元着色器中计算每一个点光源(当然还有环境光)对片元颜色的加成。并将他们全部加起来。
# Phong 光照模型
漫反射模型上的一个升级;漫反射有一个特点;没办法描述镜面反射。

specular 是高光。
漫反射可以表现出粗糙表面的光照现象,如墙壁,纸张等,但是无法很好地表现出光泽金属所有的镜面反射。
phong 模型认为镜面反射的光强与反射光线和视线的夹角相关。
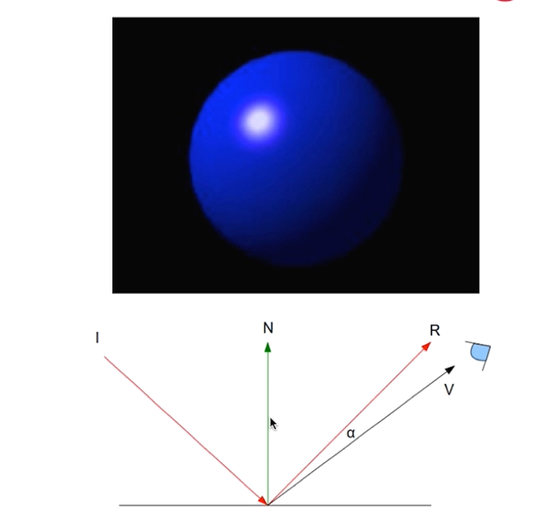
specular = Ks * lightColor * (dot(V, R))^shininess