# threeJS
threeJS 是 webgl 的封装,主要包含下面:
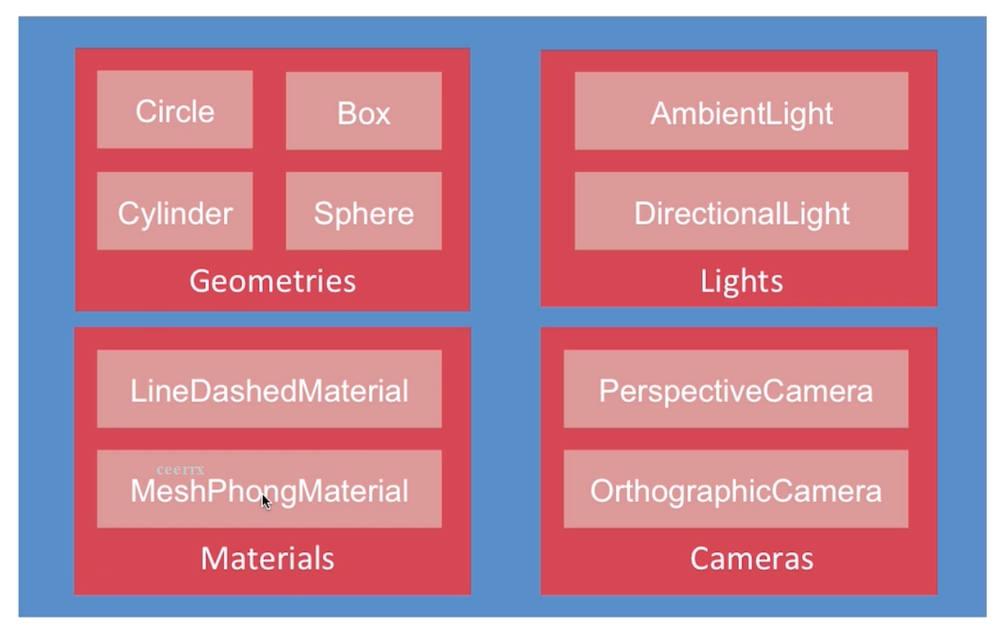
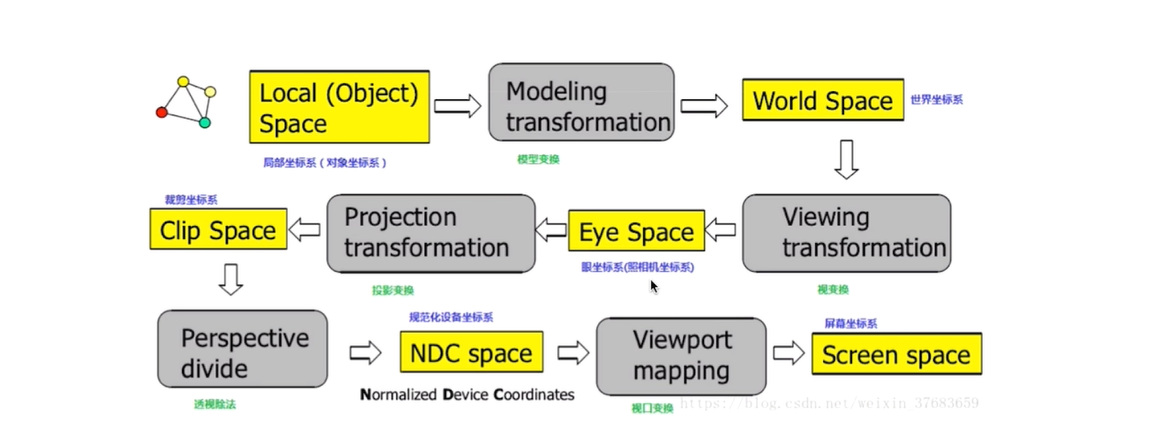
基本场景渲染:
首先每个物体都有自己的局部坐标系,比如三维场景中的一个车子,相对于局部坐标系(对象坐标系)进行绘制,然后我们需要通过模型变化(也就是平移、旋转、缩放等操作)将车子本身相对于自身的坐标转换为在三维世界中的坐标。也就是在世界坐标系下,车子的位置。然后通过视变换。视变化就是人眼(相机)所能观察的空间的坐标。也就是需要放在以相机为坐标原点的视空间下。所以世界坐标系的坐标需要转换为以人眼(相机)为中心的坐标系中。这个坐标也是最终要在 webgl 中渲染所要使用的坐标。然后需要进一步的投影变换。投影变换会限制在视空间下,物体所具有的范围,因为人眼(相机)所能观察到的物体的范围是有限的,我们根据一个近平面以及远平面限定范围。没有进入近平面或者超过远平面的物体不会进行渲染的。然后得到裁剪坐标系下的物体。在投影变换中,常用的投影方式有正交投影以及透视投影。透视投影更接近我们现实生活中,人眼观察到的情况(近大远小)。然后通过透视出发,得到规范化设备坐标系,最后通过视口变化,得到最终在屏幕坐标系下的物体的坐标。
- 模型变换及模型矩阵
- 局部(物体)坐标系或者局部(物体)空间: 物体空间比较容易理解,就是需要绘制的3D物体所在的原始坐标系代表的空间。例如在进行设计时,物体的几何中心是摆放到坐标系原点的,这个坐标系代表的就是物体空间。
- 世界坐标系或者世界空间: 世界空间也不难理解,就是物体在最终3D场景中的摆放位置对应的坐标所属的坐标系代表的空间。模型变换指的是将物体坐标系下的物体变换到世界坐标系下。模型变换通过乘以模型矩阵来实现。模型矩阵包含这平移,旋转,缩放的信息。模型矩阵也可以称作基本总变换矩阵。我们需要注意的是:模型变换针对是整个局部坐标系,或者说同一局部坐标系下的所有物体,或者说所有坐标。
- 视变化及视图矩阵
- 摄像机坐标系或者摄像机空间: 物体经摄像机观察后,进入摄像机空间。
- 视变化: 是将世界坐标系下的坐标变化到摄像机坐标系,视变换是通过乘以视图矩阵实现的。
首先,我们要知道视并不存在真正的摄像机,只不过是在世界坐标系里面选择一个点,作为摄像机的位置。然后根据一些参数,在这个点构建一个坐标系。然后通过 视图矩阵将世界坐标系的坐标变换到摄像机坐标系下。
WebGL 成像采用的是虚拟相机模型。在场景中你通过模型变换,将物体放在场景中不同位置后,最终哪些部分需要成像,显示在屏幕上,主要由视变换和后面要 介绍的投影变换、视口变换等决定。其中视变换阶段,通过假想的相机来处理矩阵计算能够方便处理。对于 WebGL 来说并不存在真正的相机,所谓的相机坐标空间(camera space 或者 eye space)只是为了方便处理,而引入的坐标空间。
- 投影变换及投影矩阵
- 剪裁坐标系或者剪裁空间: 并不是摄像机空间中所有的物体都能最终被观察到,只有在摄像机空间中位于视景体内(投影范围内)的物体才能最终被观察到。因此,将摄像机空间内视景体内的部分独立出来经过处理后就成为了剪裁空间。
投影变换是将摄像机坐标系下的物体变换到剪裁坐标系,投影变换是通过乘以投影矩阵实现。
投影方式有两种,一种是正交投影,一种透视投影。
正交投影:投影到近平面上相同尺寸大小的图形大小相同,不会有真实世界那种近大远小的感觉。
透视投影:同样尺寸的物体,近处的物体投影出来大,远处的物体投影出小,会产生与真实世界一样近大远小的感觉。
在乘以投影矩阵后,任何一个点的坐标 [x,y,z,w] 中的下x,y,z的分量将在 -w~w 内。
- 透视除法(规范化坐标)
标准设备坐标系或者标准设备空间:对剪裁空间执行透视除法后得到的就是标准设备空间了,对于 WebGL 而言标准设备空间 3 个轴的坐标范围都是 -1.0~1.0。 从剪裁坐标系到标准设备坐标系的变换是通过执行透视除法来完成的。所谓透视除法其实很简单,就是将齐次坐标 [x,y,z,w] 的4个分量都除以 w,结果为 [x/w,y/w,z/w,1],本质上就是对齐次坐标进行了规范化。
需要指出,剪裁空间之后的变换就不归开发人员管了,是由管线自动完成的。包括透视除法以及后面的视口变换。
- 视口变换
屏幕坐标系或者窗口空间:实际窗口空间也很容易理解,其一般代表的是设备屏幕上的一块矩形区域,用于呈现渲染结果,其坐标以像素为单位。
视口变换是从标准设备坐标系到屏幕坐标系变换,主要工作是将执行透视除法后的 X、Y 坐标分量转换为屏幕坐标系的 XY 像素坐标。主要的思路是将标准设备空间的 XY 平面对应到视口上,将 -1.0~1.0 范围内的 X、Y 坐标折算为视口上的像素坐标。当然,这个部分也是由管线自动完成。视口范围仅需要调用 glViewPort 这个函数进行设置即可。
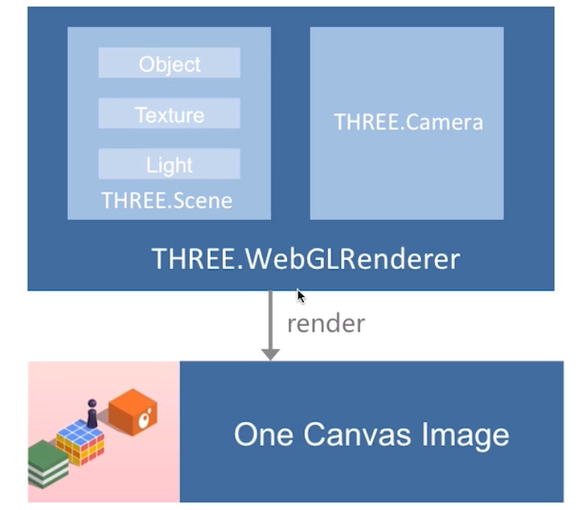
对应 threeJS 中基本场景渲染:
- THREE.WebGLRender:对应 webgl 中的视口变换;
- THREE.Scene:对应 webgl 中的局部坐标系到世界坐标系的转换;
- THREE.Camera:对应 webgl 中的视变化到投影变换之间的转换;
一个物体最终渲染出来的过程: 最终顶点坐标 = 投影矩阵 × 视图矩阵 × 模型矩阵 × 顶点坐标
# 例子-渲染三角形
渲染一个三角形代码如下:
var width = 400
var height = 400
var canvas = document.getElementById('demo-canvas')
var renderer = new THREE.WebGLRenderer({
canvas: canvas
})
// 场景
var scene = new THREE.Scene()
// 正交相机
var camera = new THREE.OrthographicCamera(-width / 2, width / 2, height / 2, -height / 2, -1000, 1000)
// 设备清空背景色
renderer.setClearColor(new THREE.Color(0x000000, 1.0))
renderer.setSize(400, 400)
// 绘制三角形
var triangleShape = new THREE.Shape()
triangleShape.moveTo(0, 100)
triangleShape.lineTo(-100, -100)
triangleShape.lineTo(100, -100)
triangleShape.lineTo(0, 100)
// 定义几何体-相当于顶点着色器
var geometry = new THREE.ShapeGeometry(triangleShape)
// 定义三角形的材质-相当于片元着色器
var material = new THREE.MeshBasicMaterial({
color: 0xff0000,
side: THREE.DoubleSide // 正反面渲染
})
// 渲染的物体
var mesh = new THREE.Mesh(geometry, material)
// 渲染的位置
mesh.position.x = 0
mesh.position.y = 0
mesh.position.z = 1
scene.add(mesh)
// 设置相机的位置
camera.position.x = 0
camera.position.y = 0
camera.position.z = 0
camera.lookAt(new THREE.Vector3(0, 0, 1))
var currentAngle = 0
var lastTimestamp = Date.now()
var animate = function () {
var now = Date.now()
var duration = now - lastTimestamp
lastTimestamp = now
currentAngle = currentAngle + duration / 1000 * Math.PI
}
var render = function () {
animate()
// 设置角度
mesh.rotation.set(0, 0, currentAngle)
// 渲染 canvas
renderer.render(scene, camera)
requestAnimationFrame(render)
}
render()
# 世界坐标系到观察者坐标系
将世界坐标系通过旋转平移至观察者坐标系,这个旋转 R 和平移 T 矩阵的组合矩阵 M = T * R ,则视图矩阵为 view = M 的逆矩阵;
视图矩阵:模型矩阵是相对时间坐标系的变化,但是大多数情况下,我们更关注物体相对于观察者的坐标变化,这决定了最终在 canvas 上渲染的结果。
# 视图矩阵
模型矩阵是相对世界坐标系的变换,但是大多数情况下,我们更关注物体相对于观察者的坐标变化,这决定了最终在 canvas 上渲染的结果

将世界坐标系通过旋转平移至观察者坐标系,这个旋转 R 和平移 T 矩阵的组合矩阵 M = T * R,则试图矩阵为 view = M 的逆矩阵。
视图矩阵推导:
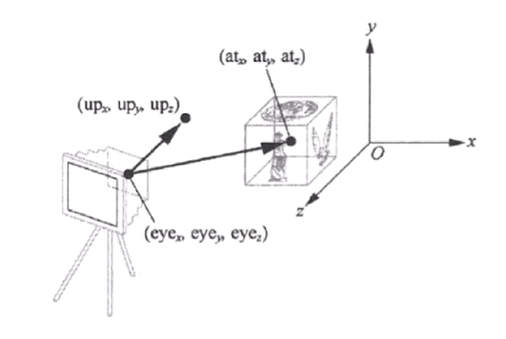
- 计算摄像机镜头方向 forwrad = (target - eye) 归一化处理 forwrad = forwrad / |forwrad| forwrad 也就是 z 轴的基向量
- 根据 up vector 和 forwrad 确定摄像机的 side 向量归一化 up vector: viewUp' = viewUp / |vieUp| 叉积:side = cross(forwrad, viewUp')
- 根据 forwrad 和 side 计算 up 向量:叉积:up = cross(side, forwrad)(注意此 up 向量是垂直于 forwrad 和 side 构成的平面)
叉乘获取的是垂直平面的向量
数学表达式

代码:
Matrix4.prototype.setLookAt = function (eyeX, eyeY, eyeZ, centerX, centerY, centerZ, upX, upY, upZ) {
var e, fx, fy,fz, rlf, sx, sy, sz, rls, ux, uy, uz;
// 1. 计算摄像机镜头方向
fx = centerY - eyeX;
fy = centerY - eyeY;
fz = centerZ - eyeZ;
// 归一化参数
rlf = 1 / Math.sqrt(fx * fx + fy * fy + fz * fz);
fx *= rlf;
fy *= rlf;
fz *= rlf;
// 2. 根据 up vector 和 forword 确定摄像机的 side 向量
sx = fy * upZ - fz * upY;
sy = fz * upX - fx * upZ;
sz = fx * upY - fy * upX;
// 归一化处理
rls = 1 / Math.sqrt(sx*sx + sy*sy + sz*sz);
sx *= rls;
sy *= rls;
sz *= rls;
// 根据 forword 和 side 计算 up 向量
ux = sy * fz - sz * fy;
uy = sz * fy - sx * fz;
uz = sx * fy - sy * fx;
// 转置矩阵
e = this.elements;
e[0] = sx; e[4] = sy; e[8] = sz; e[12] = 0;
e[1] = ux; e[5] = uy; e[9] = uz; e[13] = 0;
e[2] = -fx; e[6] = -fy; e[10] = -fz; e[14] = 0;
e[3] = 0; e[7] = 0; e[11] = 0; e[15] = 1;
// 乘以平移矩阵
return this.translate(-eyeX, -eyeY, -eyeZ);
}
Matrix4.prototype.translate = function(x, y, z) {
var e = this.elements;
e[12] += e[0] * x + e[4] * y + e[8] * z;
e[13] += e[1] * x + e[5] * y + e[9] * z;
e[14] += e[2] * x + e[6] * y + e[10] * z;
e[15] += e[3] * x + e[7] * y + e[11] * z;
return this;
}
只使用视图矩阵是不能将结果渲染出来,需要结合投影矩阵来实现映射,映射到一个规范化的坐标系中,才能得到最终的渲染效果。
# 投影矩阵
并不是摄像机空间中所有的物体都能最终被观察到,只有在摄像机空间中位于视景图内(投影范围内)的物体才能最终被观察到。因此,将摄像机空间内视景体内的部分独立出来经过处理后就成为了裁剪空间。 投影变换是将摄像机坐标系下的物体变换到剪裁坐标系,投影变换是通过乘以投影矩阵实现的。
通过投影矩阵将相机坐标系中的物体投影变化为裁剪坐标系,通常有两种投影方式,透视投影跟正交投影。
# 透视投影
透视投影分两步:
- 从 Frustun 内一点投影到近裁剪平面的过程
- 由近平面到规范化设备坐标系的过程
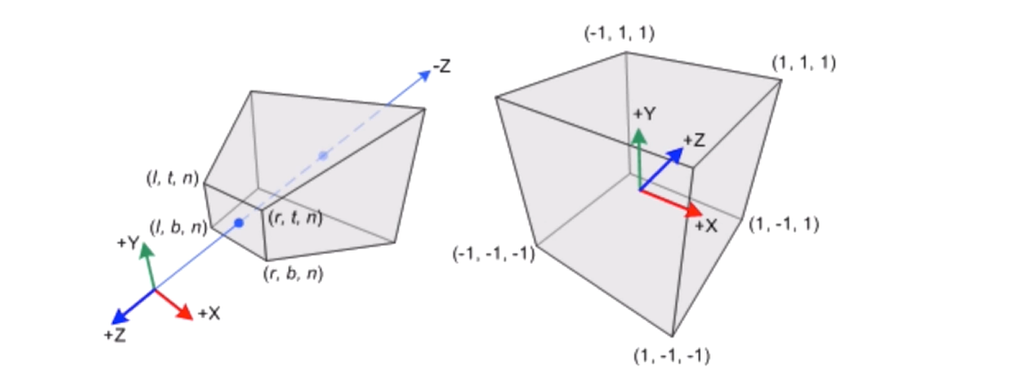
gl_Position 的第四个参数也就是缩放系数。
透视投影推导:
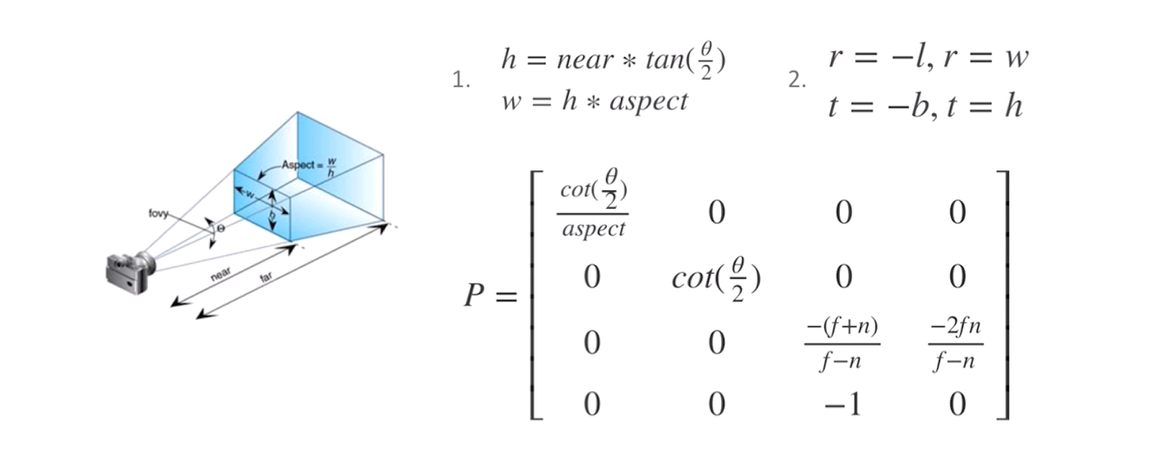
实现代码:
Matrix4.prototype.setPerspective = function (fovy, aspect, near, far) {
var e, s, ct;
if (near === far || aspect == 0) {
throw 'null frustum';
}
if (near <= 0) {
throw 'near <= 0';
}
if (far <= 0) {
throw 'far <= 0';
}
fovy = Math.PI * fovy / 180 / 2;
s = Math.sin(fovy);
if (s === 0) {
throw 'null frustum';
}
rd = 1 / (far - near);
ct = Math.cos(fovy) / s;
e = this.elements;
e[0] = ct / aspect; e[4] = 0; e[8] = 0; e[12] = 0;
e[1] = 0; e[5] = ct; e[9] = 0; e[13] = 0;
e[2] = 0; e[6] = 0; e[10] = -(far + near) / (far - near); e[14] = -2 * near * far / (far - near);
e[3] = 0; e[7] = 0; e[11] = -1; e[15] = 0;
return this;
}
# 正交投影
正交投影分两步:
- 从 Frustum 内一点投影到近裁剪平面的过程
- 由近平面到规范化设备坐标系的过程
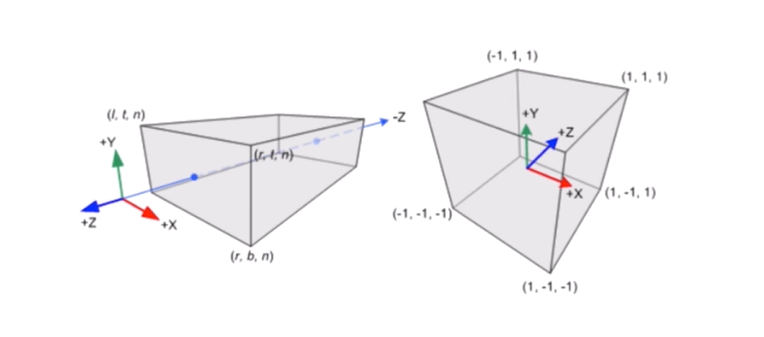
正交投影推导:

实现代码:
Matrix4.prototype.setOrtho = function(left, right, bottom, top, near, far) {
if (left === right || bottom === top || near === far) {
throw 'null frustum';
}
e = this.elements;
e[0] = 2 / (right - left); e[4] = 0; e[8] = 0; e[12] = - (right + left) / (right - left);
e[1] = 0; e[5] = 2 / (top - bottom); e[9] = 0; e[13] = - (top + bottom ) / (top - bottom);
e[2] = 0; e[6] = 0; e[10] = -2 / (far - near); e[14] = - (far + near) / (far - near);
e[3] = 0; e[7] = 0; e[11] = 0; e[15] = 1;
return this;
}
# 正交相机
这一摄像机使用orthographic projection(正交投影)来进行投影。在这种投影模式下,无论物体距离相机距离远或者近,在最终渲染的图片中物体的大小都保持不变。 这对于渲染2D场景或者UI元素是非常有用的。
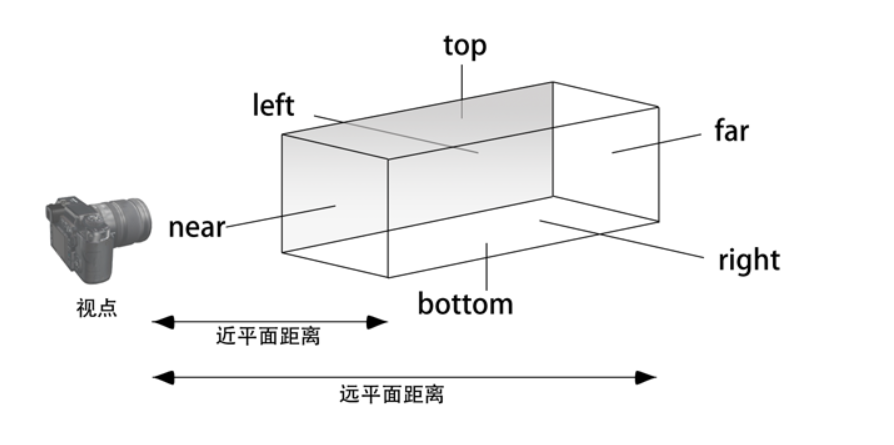
正交投影相机示意图如下:
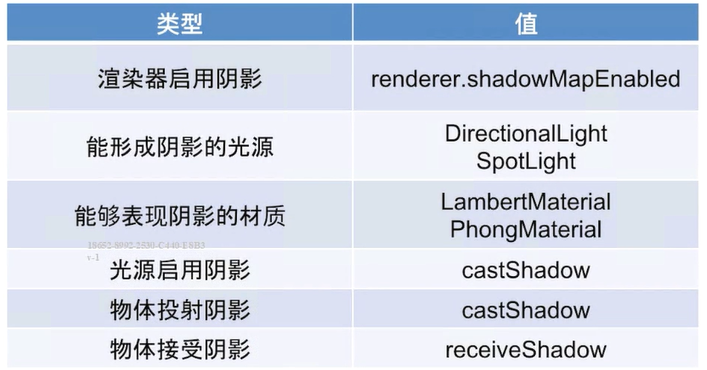
# shadow