# 矢量
矢量在地理信息系统中，具有重要角色，算法中所有的点都看做矢量，两点的加减法就是矢量相加减，而点的乘法则看做矢量叉积；
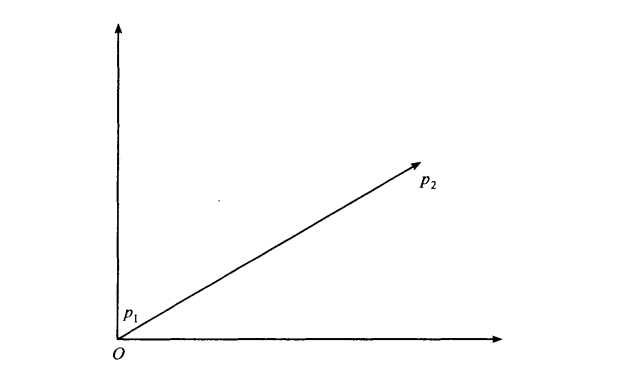
矢量也就是一种既有大小又有方向的量，又称为向量；如果一条线段的端点是有次序之分的，那这种线段称为有向线段，向量应该都很熟悉吧：
如下：有向线段 p1 p2 的起点 p1 在坐标原点，我们可以把它称为矢量 p2：
# 矢量加减法
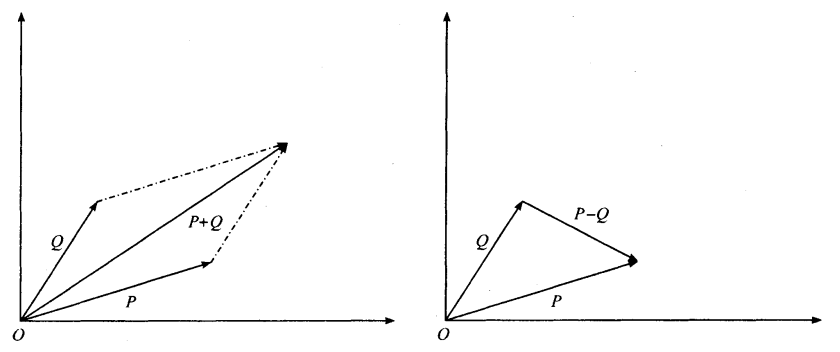
向量的加法满足平行四边形法则和三角形法则。比如二维矢量 P = (x1, y1), Q = (x2, y2)，则矢量加法定义为 P + Q = (x1 + x2, y1 + y2)，同样，矢量减法就是 P - Q = (x1 - x2, y1 - y2)，显然有性质 P + Q = Q + P, P -Q = -(Q - P):
# 矢量叉积
# 数量积
数量积也叫点积（内积），它是向量与向量的乘积，其结果为一个标量（非向量）。几何上，数量积可以定义如下：设a、b为两个任意向量，它们的夹角为，则他们的数量积为：
即 a 向量在 b 向量方向上的投影长度（同方向为正反方向为负号），与 b 向量长度的乘积。 坐标点计算：
a . b = x1x2 + y1y2
内积（点乘）的几何意义包括：
- 表征或计算两个向量之间的夹角
- b向量在a向量方向上的投影
# 向量积
向量积也叫叉积，外积，它也是向量与向量的乘积，不过需要注意的是，它的结果是个向量。它的几何意义是所得的向量与被乘向量所在平面垂直，方向由右手定则规定，大小是两个被乘向量张成的平行四边形的面积。
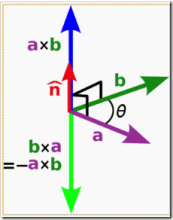
向量积可以被定义为：
模长：（在这里 θ 表示两向量之间的夹角（共起点的前提下）（0°≤θ≤180°），它位于这两个矢量所定义的平面上。）
方向：a 向量与 b 向量的向量积的方向与这两个向量所在平面垂直，且遵守右手定则。
也可以这样定义（等效）：向量积 |c|=|a×b|=|a||b|sin<a，b> 即 c 的长度在数值上等于以 a，b，夹角为 θ 组成的平行四边形的面积。而 c 的方向垂直于 a 与 b 所决定的平面，c 的指向按右手定则从 a 转向 b 来确定。
计算矢量叉积是与直线和线段相关算法的核心部分。设矢量 P = (x1, y1)，Q = (x2, y2)，则矢量叉积定义为由(0, 0)、P1、P2 和 P1P2 所组成的平行四边形的带符号的面积， 即：P × Q = x1.y2 - y2.y1，其结果是一个标量，显然有性质 P × Q = -(Q × P) 和 P × (-Q) = -(P × Q)
向量外积的几何意义：
在三维几何中，向量 P 和向量 Q 的外积结果是一个向量，有个更通俗易懂的叫法是法向量，该向量垂直于 P 和 Q 向量构成的平面。
在 3D 图像学中，外积的概念非常有用，可以通过两个向量的外积，生成第三个垂直于 P，Q 的法向量，从而构建 X、Y、Z 坐标系。
在二维空间中，外积还有另外一个几何意义就是：|a×b| 在数值上等于由向量 P 和向量 Q 构成的平行四边形的面积。
# 补充
# sinθ 曲线
# cosθ 曲线
# gis 中的应用
叉积的一个非常重要的性质是可以通过它的符号判断两矢量相互之间的顺逆时针关系：
- 如果 P × Q > 0，则 P 在 Q 的顺时针方向。
- 如果 P × Q < 0，则 P 在 Q 的逆时针方向。
- 如果 P × Q = 0，则 P 与 Q 共线，但可能同向也可能反向。
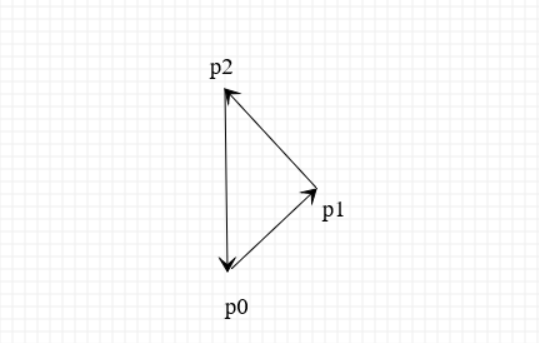
# 折线段的拐向判断
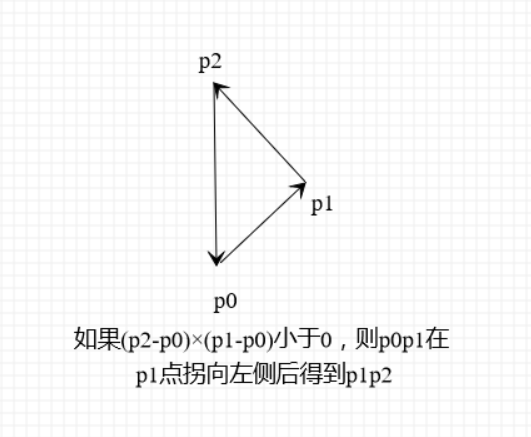
折线段的拐向判断方法可以直接由矢量叉积的性质推出。对于有公共端点的线段 p0p1 和 p1p2，通过计算 (p2 - p0) × (p1 - p0) 的符号便可以确定折线段的拐向：
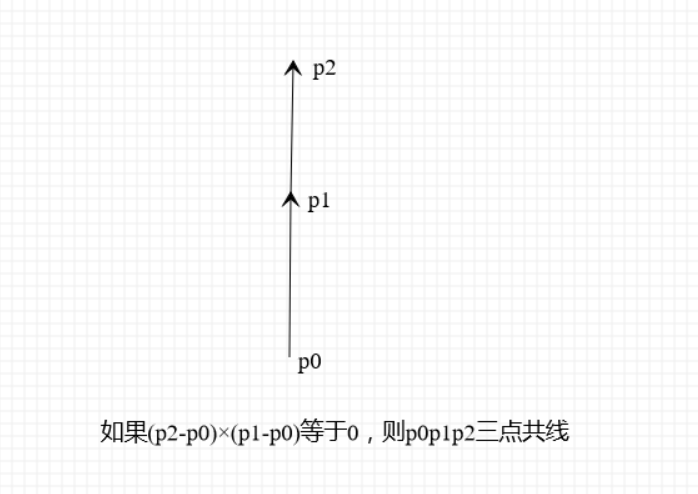
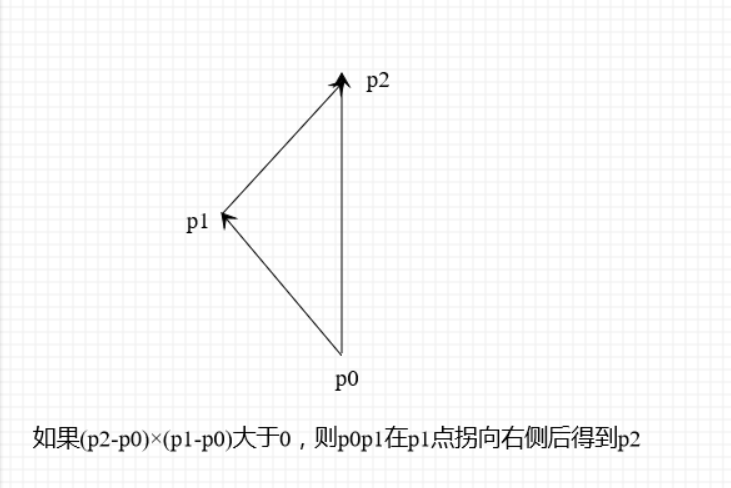
- 如果 (p2-p0)×(p1-p0) > 0，则 p0p1 在 p1 点拐向右侧后得到 p1p2。
- 如果 (p2-p0)×(p1-p0) < 0，则 p0p1 在 p1 点拐向左侧后得到 p1p2。
- 如果 (p2-p0)×(p1-p0) = 0，则 p0p1p2 三点共线。
JavaScript 实现代码
/**
* 判断三点组成的折线的拐点方向
* @param {*} pt1 点1
* @param {*} pt2 点2
* @param {*} pt3 点3
* <returns>0：直线；1：右拐；大于 0：左拐</returns>
*/
function brokenlineDirection(pt1, pt2, pt3) {
return (pt3.x - pt1.x) * (pt3.y - pt1.y) - (pt2.x - pt1.x) * (pt2.y - pt1.y);
}