# 判断两条线是否相交
# 算法一
分两步确定两条线段是否相交
| 同过快速排斥实验 | 未通过快速排斥实验 | |
|---|---|---|
| 未通过跨立实验 | ||
| 通过跨立实验 | \ |
- 快速排斥
假设线段 P1P2 为对角线的矩形为 R,设以线段 Q1Q2 为对角线的矩形为 T,如果 R 和 T 不想交,显然两线段不会相交;
- 检测跨立
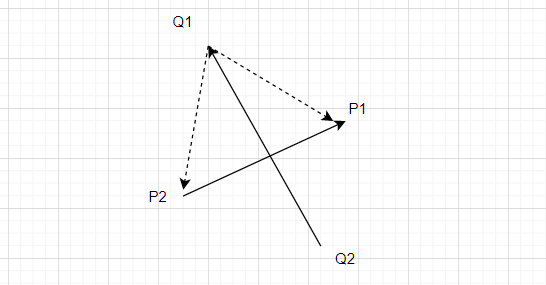
如果两线段相交,则两线段必然相互跨立对方。如果 P1P2 跨立 Q1Q2,则矢量 (P1 - Q1) 和 (P2 - Q1) 位于矢量 (Q2 - Q1) 的两侧,
也就是
(P1 - Q1) × (Q2 - Q1) × (P2 - Q1) × (Q2 - Q1) < 0
上面的式子改写成
(P1 - Q1) × (Q2 - Q1) × (Q2 - Q1) × (P2 - Q1) > 0
如果为下面的情况:
那么,P1 一定在线段 Q1Q2 上,
(P1 - Q1) × (Q2 - Q1) = 0
同理,如果满足下面的等式,说明 P2 一定在线段 Q1Q2 上。
(Q2 - Q1) × (P2 - P1) = 0
综上,如果判断 P1P2 跨立 Q1Q2 的依据是:
(P1 - Q1) × (Q2 - Q1) × (Q2 - Q1) × (P2 - Q1) >= 0
同理判断 Q1Q2 跨立 P1P2 的依据是:
(Q1 - P1) × (P2 - P1) × (P2 - P1) × (Q2 - P1) >= 0
实现代码:
/**
* 判断两条线是否相交,如果相交返回交点
*
* @private
* @param line1 线 1 坐标点数组
* @param line2 线 2 坐标点数组
* @returns true 相交, false 不相交
*/
function intersects(line1, line2) {
const x1 = line1[0][0]
const y1 = line1[0][1]
const x2 = line1[1][0]
const y2 = line1[1][1]
const x3 = line2[0][0]
const y3 = line2[0][1]
const x4 = line2[1][0]
const y4 = line2[1][1]
// 快速排斥
if(!(Math.min(x1, x2) <= Math.max(x3, x4) && Math.min(y3, y4) <= Math.max(y1, y2) && Math.min(x3, x4) <= Math.max(x1, x2) && Math.min(y1, y2) <= Math.max(y3, y4)))
return false
// 跨立实验
let u, v, w, z
u = (x3 - x1) * (y2 - y1) - (x2 - x1) * (y3 - y1)
v = (x4 - x1) * (y2 - y1) - (x2 - x1) * (y4 - y1)
w = (x1 - x3) * (y4 - y3) - (x4 - x3) * (y1 - y3)
z = (x2 - x3) * (y4 - y3) - (x4 - x3) * (y2 - y3)
return (u * v <= 0.00000001 && w * z <= 0.00000001)
}
# 算法二
定义 A,B,C,D 为二维空间的点,则有向线段 AB 和 CD 的参数方程为:
AB = A + r(B - A), r∈[0, 1]
CD = C + s(D - C), s∈[0, 1]
如果 AB 与 CD 相交,则两条直线必有交点:
A + r(B - A) = C + s(D - C) => Ax + r(Bx - Ax) = Cx + s(Dx - Cx), Ay + r(By - Ay) = Cy + s(Dy - Cy)
# 解方程,求 r 和 s
r = ((Ay - Cy)(Dx - Cx) - (Ax - Cx)(Dy - Cy)) / ((Bx - Ax)(Dy - Cy) - (By - Ay)(Dx - Cx))
s = ((Ay - Cy)(Bx - Ax) - (Ax - Cx)(By - Ay)) / ((Bx - Ax)(Dy - Cy) - (By - Ay)(Dx - Cx))
设 P 为直线 AB 和 CD 的交点则:
P = A + r(B - A) => Px = Ax + r(Bx - Ax),Py = Ay + r(By - Ay)
如果(0 <= r <= 1)并且(0 <= s <= 1)那么有向线段 AB 和 CD 的交点存在,否则交点不存在
/**
* 判断两条线是否相交,如果相交返回交点
*
* @private
* @param line1 线 1 坐标点数组
* @param line2 线 2 坐标点数组
* @returns 相交的点数组
*/
function intersects(line1, line2) {
if (line1.length !== 2) {
throw new Error('line1 must only contain 2 coordinates')
}
if (line2.length !== 2) {
throw new Error('line2 must only contain 2 coordinates')
}
const x1 = line1[0][0]
const y1 = line1[0][1]
const x2 = line1[1][0]
const y2 = line1[1][1]
const x3 = line2[0][0]
const y3 = line2[0][1]
const x4 = line2[1][0]
const y4 = line2[1][1]
const denom = ((y4 - y3) * (x2 - x1)) - ((x4 - x3) * (y2 - y1))
const numeA = ((x4 - x3) * (y1 - y3)) - ((y4 - y3) * (x1 - x3))
const numeB = ((x2 - x1) * (y1 - y3)) - ((y2 - y1) * (x1 - x3))
if (denom === 0) {
if (numeA === 0 && numeB === 0) {
return null
}
return null
}
const uA = numeA / denom
const uB = numeB / denom
if (uA >= 0 && uA <= 1 && uB >= 0 && uB <= 1) {
const x = x1 + (uA * (x2 - x1))
const y = y1 + (uA * (y2 - y1))
return [x, y]
}
return null
}
阅读量: