投影矩阵分为正交投影矩阵（正射投影矩阵）以及透视投影矩阵；

投影变换完成的是如何将三维模型显示到二维视口上，这是一个三维到二维的过程。你可以将投影变换看作是调整照相机的焦距，它模拟了为照相机选择镜头的过程。投影变换是所有变换中最复杂的一个。

透视投影推导

透视投影是为了模拟人眼的近大远小的一个特性。

视椎体

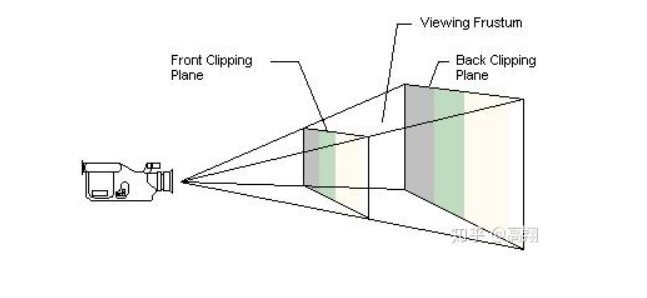
视锥体是一个三维体，他的位置和摄像机相关，视锥体的形状决定了模型如何从视空间投影到屏幕上。透视投影使用棱锥作为视锥体，摄像机位于棱锥的椎顶。该棱锥被前后两个平面截断，形成一个棱台，叫做 View Frustum，只有位于 Frustum 内部的模型才是可见的。我们也通常称这个为裁剪空间，在这个裁剪空间中有两个平面比较特殊，我们分辨称为近裁剪平面（near clip plane）和远裁剪平面（far clip plane）。

投影矩阵的本质

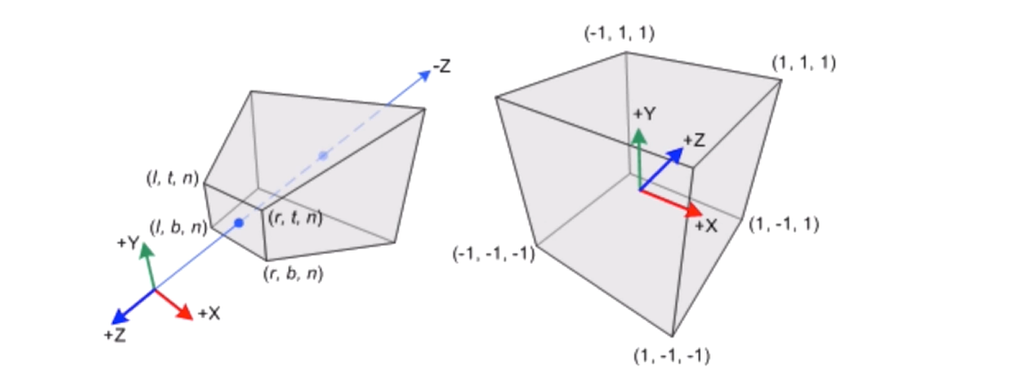
投影矩阵有两个目的： - 首先是为投影做准备。这是个迷惑点。虽然投影矩阵的名称包含了投影二字，但是它并没有进行真正的投影工作，而是在为投影做准备。真正得投影发生在后面得齐次除法（homogeneous division）过程中。经过投影矩阵的变换后，顶点的 w 分量会具有特殊的意义。 - 其次是对 x ，y，z 分量进行缩放。如果用视锥体的6个裁剪平面来进行裁剪会比较麻烦，而经过投影矩阵的缩放后，就可以直接使用 w 分量作为一个范围值。如果 x ，y，z 分量都位于这个范围内，就说明该顶点位于裁剪空间内，如下图所示

图1：

投影矩阵推导

透视投影分两步：

1. 从 Frustun（视椎） 内一点投影到近裁剪平面的过程
2. 由近平面到规范化设备坐标系的过程（透视除法- webgl 底层实现）

我们最后得到的 gl_Position 的坐标并不是规范化设置坐标系的坐标。 但是这个坐标带有一个 w 的值，w 值代表近大远小的一个属性。webgl 可以通过这个值进行会规范化坐标。gl_Position 是一个 vec4 类型的数据，第四个参数也就是缩放系数。

投影矩阵的推导目标：

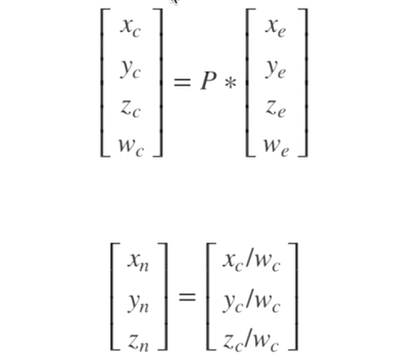
P 是透视投影矩阵，通过与坐标点进行计算得到（xc, yc, zc, wc）的视空间下的物体坐标。然后通过 xc / wc 等操作进行规范化系内的坐标。

将相机坐标系中的点 p = (xe, ye, ze) 投影到投影平面，得到点：p' = (xp, yp, -nearVal)

在俯视图中，可以看到两个相似三角形，xp/xe = -n/ze，所以 xp 就等于 - (xe*n) / ze；从侧视图可以得到 yp = -(ye * n) / ze；我们可以看到 xp 与 yp 都是除了 -ze，所以我们可以看到最终的 w（缩放系数）为 -ze^1。这样就得到了下图右侧矩阵：

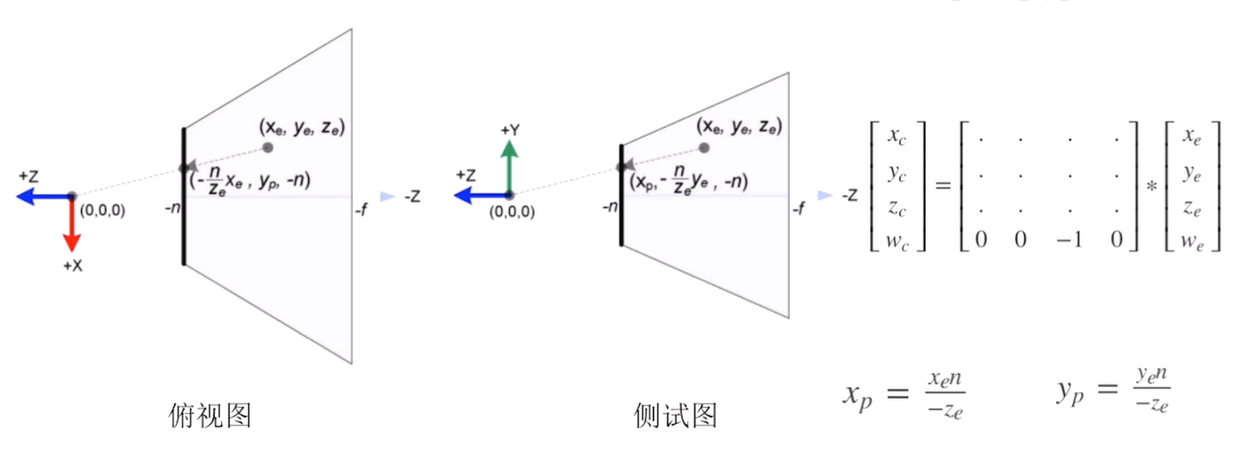
接下来就是将近平面中的坐标映射到 webgl 坐标系下；由 xp（近裁剪平面上的投影坐标） 映射到 xn（规范化设备坐标系中的坐标）； 将图 1 中的 l（近裁剪平面的左边） 点会映射到 -1，将 r（近裁剪平面的右边） 点映射到 +1。

xp 的范围是[l, r]，xn 的范围是 [-1, 1]，可以利用简单的线性插值的方式获得以下关系式。

然后根据上面的式子以及前面推导的 xp 的结果带入，得到下面的结果：

根据前面的 w 假设为 -ze^1，得到 xc 以及 yc

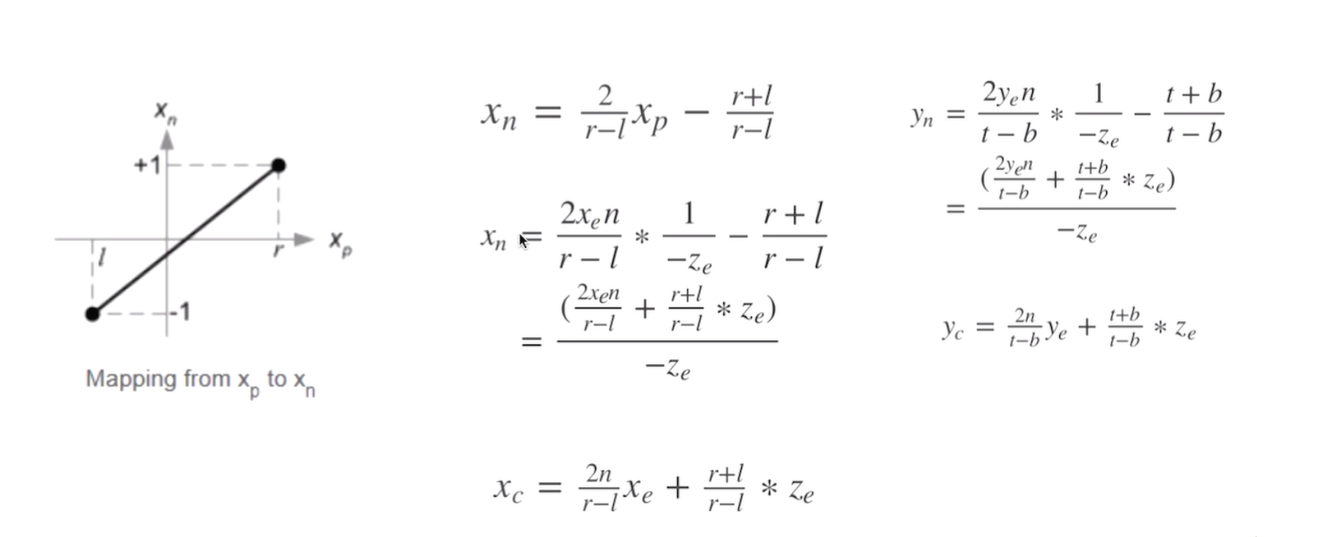
然后我们得到了下面的一个 p 矩阵：

最后看看 zn ，当视锥体内的顶点投影到近裁剪平面（near clip plane）的时候，实际上 zp 的值已经没有意义了，因为所有近裁剪平面（near clip plane）上的点，他们的 zp 值都是 -n，看起来我们甚至可以抛弃这个 zp 值，可以么？当然不行！不要忘记还有深度测试。 xe、ye、ze）最小的，所以 zp 可以直接保存为 ze 的值。由于在光栅化的过程中，要进行 z 坐标的倒数的插值，因此映射函数应为 1 / z 的函数，同时允许深度投影是线性插值，则可以获得以下映射函数 zn 的表达式：

利用 zn 与 ze 的映射关系为：(-n, -1) 和 (-f, 1)

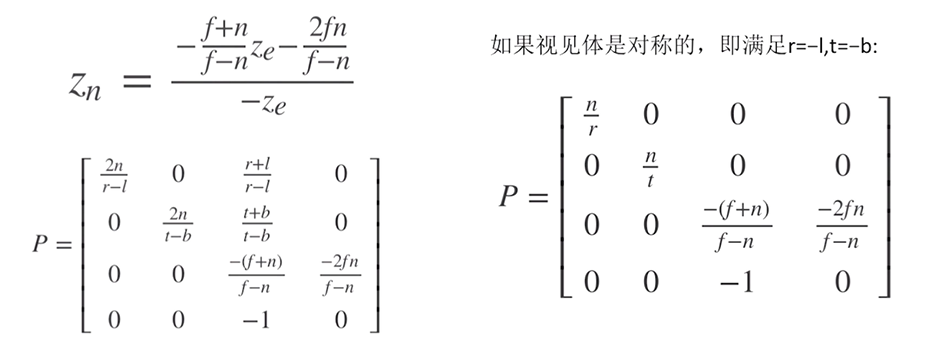
上面式子中的一些参数替换后，如下：

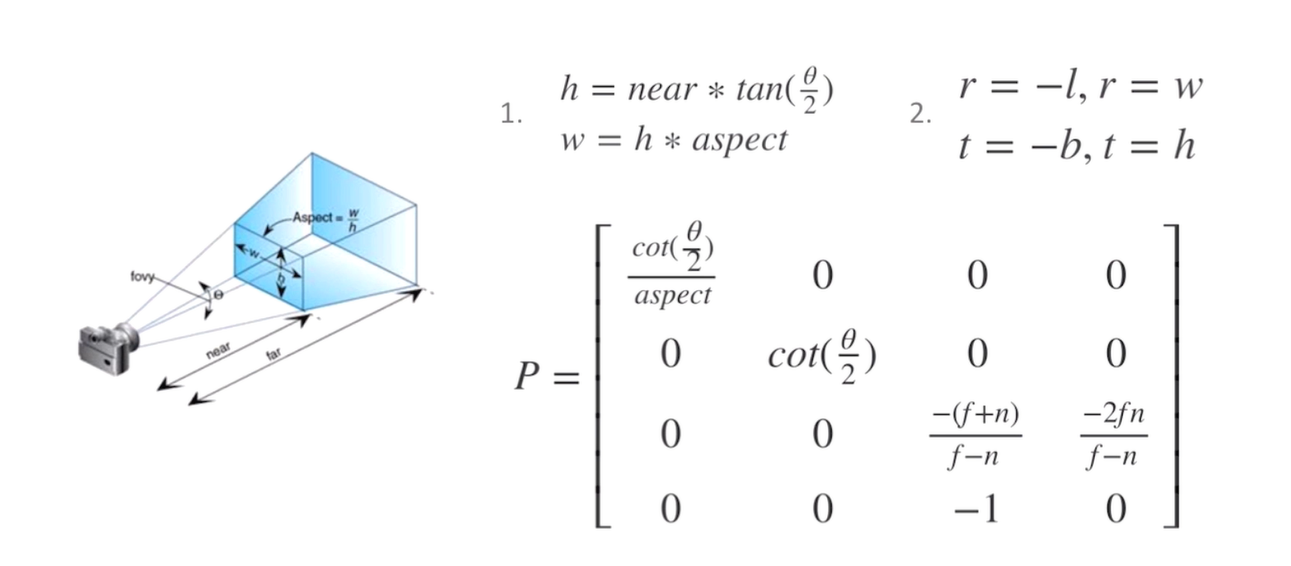
参考：https://zhuanlan.zhihu.com/p/181696883

正交投影推导

xe, ye, ze 相机中的坐标 xp、yp、zp 近裁剪平面（near clip plane）上的投影坐标 xn、yn、zn 规范化设备坐标系（Normalized Device Coordinates）中的坐标

正交投影分两步：

1. 从 Frustum 内一点投影到近裁剪平面的过程
2. 由近平面到规范化设备坐标系的过程

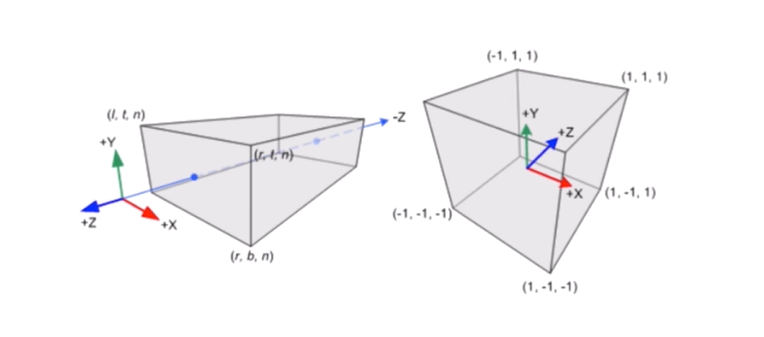
根据上面的关系，推导如下：

示例代码

透视投影

Matrix4.prototype.perspective = function(fovy, aspect, near, far) {
  // 作用在当前已有的矩阵上
  return this.concat(new Matrix4().setPerspective(fovy, aspect, near, far));
};
/**
 * 计算透视投影矩阵
 * @param fovy 视锥的上，下侧之间的角度。
 * @param aspect 视锥的长宽比. (width/height)
 * @param near 到近裁剪平面的距离，必须为正值.
 * @param far 远裁剪平面的距离，必须为正值.
 * @return this
 */
Matrix4.prototype.setPerspective = function(fovy, aspect, near, far) {
  var e, rd, s, ct;

  if (near === far || aspect === 0) {
    throw 'null frustum';
  }
  if (near <= 0) {
    throw 'near <= 0';
  }
  if (far <= 0) {
    throw 'far <= 0';
  }

  // 角度转换为弧度制
  fovy = Math.PI * fovy / 180 / 2;

  s = Math.sin(fovy);
  // fovy 没有视空间
  if (s === 0) {
    throw 'null frustum';
  }

  rd = 1 / (far - near);
  ct = Math.cos(fovy) / s;

  e = this.elements;

  e[0]  = ct / aspect;
  e[1]  = 0;
  e[2]  = 0;
  e[3]  = 0;

  e[4]  = 0;
  e[5]  = ct;
  e[6]  = 0;
  e[7]  = 0;

  e[8]  = 0;
  e[9]  = 0;
  e[10] = -(far + near) * rd;
  e[11] = -1;

  e[12] = 0;
  e[13] = 0;
  e[14] = -2 * near * far * rd;
  e[15] = 0;

  return this;
};

Matrix4.prototype.concat = function(other) {
  var i, e, a, b, ai0, ai1, ai2, ai3;
  
  // Calculate e = a * b
  e = this.elements;
  a = this.elements;
  b = other.elements;
  
  // If e equals b, copy b to temporary matrix.
  if (e === b) {
    b = new Float32Array(16);
    for (i = 0; i < 16; ++i) {
      b[i] = e[i];
    }
  }
  
  for (i = 0; i < 4; i++) {
    ai0=a[i];  ai1=a[i+4];  ai2=a[i+8];  ai3=a[i+12];
    e[i]    = ai0 * b[0]  + ai1 * b[1]  + ai2 * b[2]  + ai3 * b[3];
    e[i+4]  = ai0 * b[4]  + ai1 * b[5]  + ai2 * b[6]  + ai3 * b[7];
    e[i+8]  = ai0 * b[8]  + ai1 * b[9]  + ai2 * b[10] + ai3 * b[11];
    e[i+12] = ai0 * b[12] + ai1 * b[13] + ai2 * b[14] + ai3 * b[15];
  }
  
  return this;
};

正射投影

/**
 * 设置正交投影矩阵.
 * @param left 剪裁平面左侧的坐标.
 * @param right 剪裁平面右侧的坐标.
 * @param bottom 裁剪平面底部的坐标.
 * @param top 裁剪平面的顶部坐标.
 * @param near 近裁剪平面的距离。如果平面要在查看器后面，则此值为负.
 * @param far 远裁剪平面的距离。如果平面要在查看器后面，则此值为负.
 * @return this
 */
Matrix4.prototype.setOrtho = function(left, right, bottom, top, near, far) {
  var e, rw, rh, rd;

  if (left === right || bottom === top || near === far) {
    throw 'null frustum';
  }

  rw = 1 / (right - left);
  rh = 1 / (top - bottom);
  rd = 1 / (far - near);

  e = this.elements;

  e[0]  = 2 * rw;
  e[1]  = 0;
  e[2]  = 0;
  e[3]  = 0;

  e[4]  = 0;
  e[5]  = 2 * rh;
  e[6]  = 0;
  e[7]  = 0;

  e[8]  = 0;
  e[9]  = 0;
  e[10] = -2 * rd;
  e[11] = 0;

  e[12] = -(right + left) * rw;
  e[13] = -(top + bottom) * rh;
  e[14] = -(far + near) * rd;
  e[15] = 1;

  return this;
};

Matrix4.prototype.ortho = function(left, right, bottom, top, near, far) {
  return this.concat(new Matrix4().setOrtho(left, right, bottom, top, near, far));
};

阅读量：

评 论：