视图矩阵

我们需要将世界坐标系转换到观察者坐标系中；通过视图矩阵可以进行坐标系的变换。

模型矩阵是相对世界坐标系的变换，但是大多数情况下，我们更关注物体相对于观察者的坐标变化，这决定了最终在 canvas 上渲染的结果

将世界坐标系通过旋转平移至观察者坐标系，这个旋转 R 和平移 T 矩阵的组合矩阵 M = T * R，则视图矩阵为 view = M 的逆矩阵。

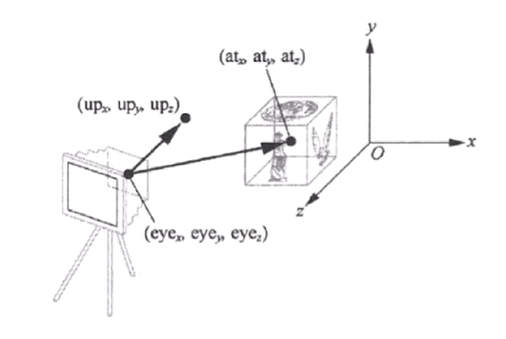
首先我们看下图，左侧的是相机坐标系的位置，右侧是物体在世界坐标系的位置，我们需要变换将世界坐标系转换为观察者坐标系下；所有的物体都相对于观察者的位置。

• 视点：(eyex, eyey, eyez) 表示相机坐标
• 观察目标点: (atx, aty, atz)
• 上方向：(upx, upy, upz)

根据上面三个分量就确定了观察者的状态。也是根据这三个矢量来创建一个视图矩阵。然后将该矩阵传给顶点着色器。之所以称为视图矩阵，是因为它最终影响了显示在屏幕上的视图，也就是观察者观察到的场景。

然后我们需要将物体的坐标转换到以视点、观察目标点、上方向这三个基量组成的坐标系中。根据下面的步骤：

1. 计算摄像机镜头方向 forwrad = (target - eye) 归一化处理 forwrad = forwrad / |forwrad| forwrad 也就是 z 轴的基向量
2. 根据 up vector 和 forwrad 确定摄像机的 side 向量归一化 up vector: viewUp' = viewUp / |vieUp| 叉积：side = cross(forwrad, viewUp') side 向量也就是垂直于 up 以及 forward 向量。
3. 根据 forwrad 和 side 计算 up 向量：叉积：up = cross(side, forwrad)(注意此 up 向量是垂直于 forwrad 和 side 构成的平面)也就是原始的 up 向量在垂直于 side 跟 forward 方向的 投影。

叉乘获取的是垂直平面的向量

数学表达式推导： 先通过平移矩阵进行变换，然后进行通过基变换得到在视空间下的坐标。

示例代码

Matrix4.prototype.setLookAt = function(eyeX, eyeY, eyeZ, centerX, centerY, centerZ, upX, upY, upZ) {
  var e, fx, fy, fz, rlf, sx, sy, sz, rls, ux, uy, uz;

  // forward 向量 
  fx = centerX - eyeX;
  fy = centerY - eyeY;
  fz = centerZ - eyeZ;

  //  forward 归一化
  rlf = 1 / Math.sqrt(fx*fx + fy*fy + fz*fz); // 向量的模
  fx *= rlf;
  fy *= rlf;
  fz *= rlf;

  // side 向量- forward 与 up 向量的叉乘
  sx = fy * upZ - fz * upY;
  sy = fz * upX - fx * upZ;
  sz = fx * upY - fy * upX;

  // 归一化 side 向量
  rls = 1 / Math.sqrt(sx*sx + sy*sy + sz*sz);
  sx *= rls;
  sy *= rls;
  sz *= rls;

  // 通过叉乘得到垂直于 forward 以及 side 向量.
  ux = sy * fz - sz * fy;
  uy = sz * fx - sx * fz;
  uz = sx * fy - sy * fx;

  // 转置矩阵
  e = this.elements;
  e[0] = sx;
  e[1] = ux;
  e[2] = -fx;
  e[3] = 0;

  e[4] = sy;
  e[5] = uy;
  e[6] = -fy;
  e[7] = 0;

  e[8] = sz;
  e[9] = uz;
  e[10] = -fz;
  e[11] = 0;

  e[12] = 0;
  e[13] = 0;
  e[14] = 0;
  e[15] = 1;

  // 平移矩阵的逆矩阵 乘以转置矩阵
  return this.translate(-eyeX, -eyeY, -eyeZ);
};

Matrix4.prototype.translate = function(x, y, z) {
  var e = this.elements;
  e[12] += e[0] * x + e[4] * y + e[8]  * z;
  e[13] += e[1] * x + e[5] * y + e[9]  * z;
  e[14] += e[2] * x + e[6] * y + e[10] * z;
  e[15] += e[3] * x + e[7] * y + e[11] * z;
  return this;
};

视图变换只是将模型坐标转换为了基于视空间下的坐标；还得需要基于投影变换，进行规范化坐标，最终进行渲染。

阅读量：

评 论：