定义

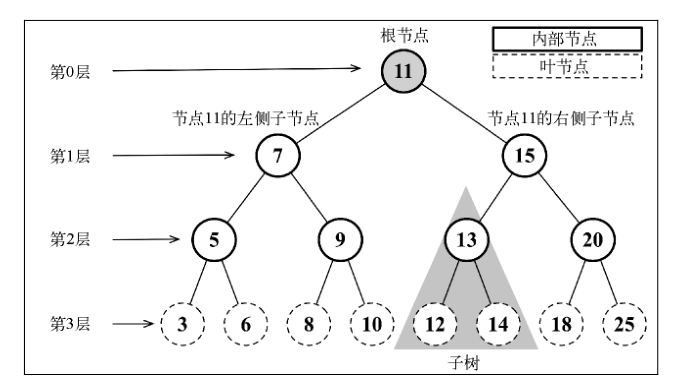
• 一种分层数据的抽象模型。
• 前端工作中常见的树包括：DOM 树，级联选择、树形控件等等。
• 一个数结构包含一系列存在父子关系的节点，每个节点都有一个父节点（除了顶部的第一个节点）以及零个或多个子节点。

深度/广度优先遍历

深度优先遍历 (DFS)

深度优先遍历：尽可能深的搜索树的分支。类似于我们读书，首先看到章节目录，然后逐个看目录里面的内容。直到看完为止。

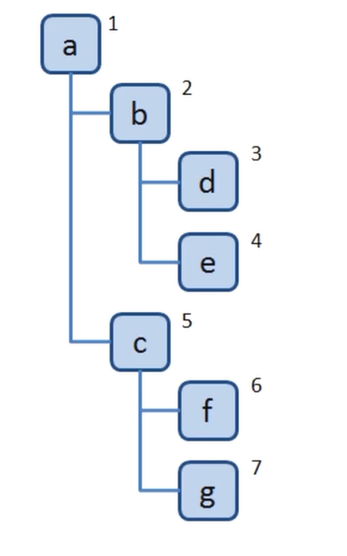
深度优先遍历算法有以下要点：

• 访问根节点。
• 对根节点的 children 挨个进行深度优先遍历。

代码实现：

const tree = {
  val: 'a',
  children: [
    {
      val: 'b',
      children: [
        {
          val: 'd',
          children: [],
        },
        {
          val: 'e',
          children: [],
        }
      ],
    },
    {
      val: 'c',
      children: [
        {
          val: 'f',
          children: [],
        },
        {
          val: 'g',
          children: [],
        }
      ],
    }
  ],
}

const dfs = (root) => {
  console.log(root.val)
  root.children.forEach(dfs)
}

dfs(tree)

广度优先遍历 (BFS)

广度优先遍历：先访问离根节点最近的节点。类似我们刚开始看书的总体目录，看完之后，然后每个章节进行深入去看。

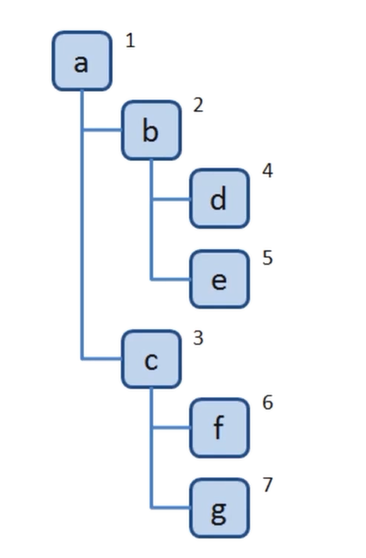
广度优先遍历算法有以下要点：

• 新建一个队列，把根节点入队。
• 把队头出队并访问。
• 把队头的 children 挨个入队。
• 重复第二、三步，直到队列为空。

代码实现：

const bfs = (root) => {
  const q = [root]
  while(q.length > 0) {
    const n = q.shift()
    console.log(n.val)
    n.children.forEach(child => {
      q.push(child)
    })
  }
}

bfs(tree)

二叉树的先中后序遍历

• 树中每个节点最多只能有两个子节点。
• 在 JS 中通常用 Object 来模拟二叉树。

先序遍历算法

• 访问根节点。
• 对根节点的左子树进行先序遍历。
• 对根节点的右子树进行先序遍历。

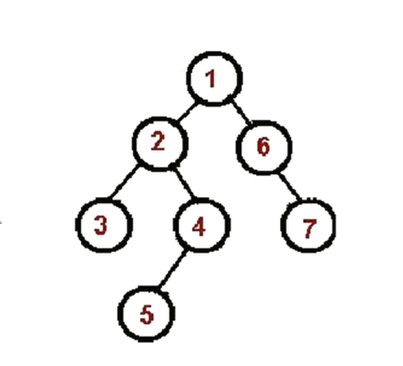
实现代码：

// bt
const bt = {
  val: 1,
  left: {
    val: 2,
    left: {
      val: 4,
      left: null,
      right: null
    },
    right: {
      val: 5,
      left: null,
      right: null
    }
  },
  right: {
    val: 3,
    left: {
      val: 6,
      left: null,
      right: null
    },
    right: {
      val: 7,
      left: null,
      right: null
    }
  }
}

module.exports = bt

const bt = require('./bt')

const preorder = (root) => {
  if (!root) return
  console.log(root.val)
  preorder(root.left)
  preorder(root.right)
}

preorder(bt)

中序遍历算法

• 对根节点的左子树进行中序遍历。
• 访问根节点。
• 对根节点的右子树进行中序遍历。

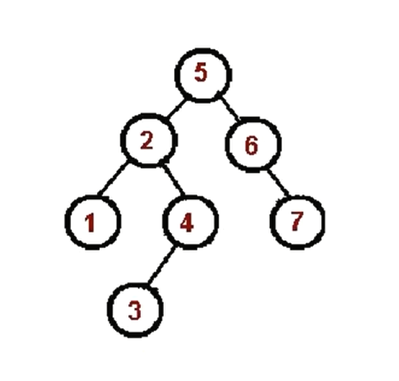
实现代码：

const bt = require('./bt')

const inorder = (root) => {
  if (!root) return
  inorder(root.left)
  console.log(root.val)
  inorder(root.right)
}

inorder(bt)

后序遍历算法

• 对根节点的左子树进行后序遍历。
• 对根节点的右子树进行后序遍历。
• 访问根节点。

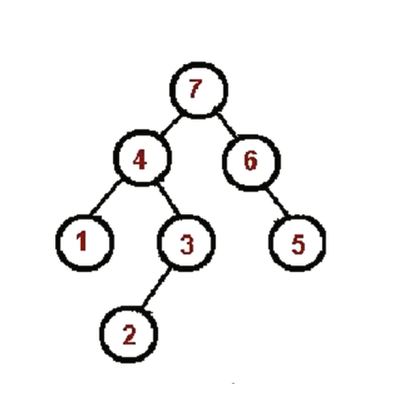
实现代码：

const bt = require('./bt')

const postorder = (root) => {
  if (!root) return
  postorder(root.left)
  postorder(root.right)
  console.log(root.val)
}

postorder(bt)

二叉树的先中后序遍历 (非递归版)

先序遍历

const preorder = (root) => {
  if (!root) return
  // 函数调用堆栈
  const stack = [root]
  while(stack.length) {
    const n = stack.pop()
    console.log(n.val)
    if (n.right) stack.push(n.right)
    if (n.left) stack.push(n.left)
  }
}

中序遍历

const inorder = (root) => {
  if (!root) return
  const stack = []
  let p = root
  while(stack.length || p) {
    while(p) {
      stack.push(p)
      p = p.left
    }
    const n = stack.pop()
    console.log(n.val)
    p = n.right
  }
}

后序遍历

就是先序遍历的倒序输出；

const postorder = (root) => {
  if (!root) return
  // 函数调用堆栈
  const stack = [root]
  const outoutStack = []
  while(stack.length) {
    const n = stack.pop()
    outoutStack.push(n)
    if (n.right) stack.push(n.right)
    if (n.left) stack.push(n.left)
  }
  while(outoutStack.length) {
    const n = outoutStack.pop()
    console.log(n.val)
  }
}

使用场景

二叉树的最大深度

给定一个二叉树，找出其最大深度。

二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。

说明: 叶子节点是指没有子节点的节点。

示例： 给定二叉树 [3,9,20,null,null,15,7]，

    3
   / \
  9  20
    /  \
   15   7

返回它的最大深度 3 。

链接：https://leetcode-cn.com/problems/maximum-depth-of-binary-tree

• 解题思路：求最大深度，考虑使用深度优先遍历。在深度优先遍历过程中，记录每个节点所在的层级，找出最大的层级即可。
• 解题步骤：新建一个变量，记录最大深度。然后深度优先遍历整棵树，并记录每个节点的层级，同时不断刷新最大深度这个变量；遍历结束返回最大深度变量。

/**
 * Definition for a binary tree node.
 * function TreeNode(val) {
 *     this.val = val;
 *     this.left = this.right = null;
 * }
 */
/**
 * @param {TreeNode} root
 * @return {number}
 */
var maxDepth = function(root) {
    let res = 0
    const dfs = (n, l) => {
        if (!n) return
        if (!n.left && !n.right) {
            res = Math.max(res, l)
        }
        dfs(n.left, l +1)
        dfs(n.right, l + 1)
    }
    dfs(root, 1)
    return res
};

二叉树的最小深度(最短路径算法)

给定一个二叉树，找出其最小深度。

最小深度是从根节点到最近叶子节点的最短路径上的节点数量。

说明：叶子节点是指没有子节点的节点。

https://leetcode-cn.com/problems/minimum-depth-of-binary-tree/

• 解题思路：求最小深度，使用广度优先遍历；在广度优先遍历过程中，遇到叶子节点，停止遍历，返回节点层次。
• 解题步骤：广度优先遍历整棵树，并记录每个节点的层级，遇到叶子节点，返回节点层级，停止遍历。

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {number}
 */
var minDepth = function(root) {
    if (!root) return 0;
    const stack = [[root, 1]];
    while(stack.length) {
        const [n, l] = stack.shift();
        if (!n.left && !n.right) {
            return l;
        };
        if (n.left) stack.push([n.left, l+1]);
        if (n.right) stack.push([n.right, l+1]);
    };
};

二叉树的层序遍历

给你一个二叉树，请你返回其按层序遍历得到的节点值。（即逐层地，从左到右访问所有节点）。

示例： 二叉树：[3,9,20,null,null,15,7],

    3
   / \
  9  20
    /  \
   15   7

返回其层次遍历结果：

[
  [3],
  [9,20],
  [15,7]
]

https://leetcode-cn.com/problems/binary-tree-level-order-traversal

• 解题思路：层序遍历顺序就是广度优先遍历，不过在遍历时候需要记录当前节点所处的层级，方便将其添加到不同的数组中。
• 解题步骤：广度优先遍历二叉树，遍历过程中，记录每个节点的层级，并将其添加到不同的数组中。

第一种：

/**
 * Definition for a binary tree node.
 * function TreeNode(val) {
 *     this.val = val;
 *     this.left = this.right = null;
 * }
 */
/**
 * @param {TreeNode} root
 * @return {number[][]}
 */
var levelOrder = function(root) {
    if (!root) return [];
    const q = [[root, 0]];
    const res = [];
    while(q.length) {
        const [n, level] = q.shift();
        if (!res[level]) {
            res.push([n.val]);
        } else {
            res[level].push(n.val);
        }
        if (n.left) q.push([n.left, level + 1]);
        if (n.right) q.push([n.right, level + 1]);
    }
    return res;
};

第二种：

/**
 * Definition for a binary tree node.
 * function TreeNode(val) {
 *     this.val = val;
 *     this.left = this.right = null;
 * }
 */
/**
 * @param {TreeNode} root
 * @return {number[][]}
 */
var levelOrder = function(root) {
    if (!root) return [];
    const q = [root];
    const res = [];
    while(q.length) {
        let len = q.length;
        res.push([])
        // 循环当前节点的所有子节点
        while(len--) {
            const n = q.shift();
            res[res.length - 1].push(n.val);
            if (n.left) q.push(n.left);
            if (n.right) q.push(n.right);
        }
    }
    return res;
};

二叉树的中序遍历

给定一个二叉树的根节点 root ，返回它的中序遍历。

https://leetcode-cn.com/problems/binary-tree-inorder-traversal/submissions

递归版：

var inorderTraversal = function(root) {
    if (!root) return []
    const res = [];
    const rec = (n) => {
        if (!n) return;
        rec(n.left);
        res.push(n.val);
        rec(n.right);
    }
    rec(root);
    return res;
};

非递归版(栈实现)：

var inorderTraversal = function(root) {
    if (!root) return [];
    const res = [];
    const stack = [];
    let p = root;
    while(stack.length || p) {
        while(p) {
            stack.push(p);
            p = p.left;
        }
        const n = stack.pop();
        res.push(n.val);
        p = n.right;
    }
    return res
};

路径总和

给定一个二叉树和一个目标和，判断该树中是否存在根节点到叶子节点的路径，这条路径上所有节点值相加等于目标和。

说明: 叶子节点是指没有子节点的节点。

示例:  给定如下二叉树，以及目标和 sum = 22，

              5
             / \
            4   8
           /   / \
          11  13  4
         /  \      \
        7    2      1

返回 true, 因为存在目标和为 22 的根节点到叶子节点的路径 5->4->11->2。

链接：https://leetcode-cn.com/problems/path-sum

• 解题思路：在深度优先遍历的过程中，记录当前路径的节点的和。
• 解题步骤：深度优先遍历二叉树，在叶子节点处，判断当前路径的节点值的和是否等于目标值，是就返回 true。遍历结束，如果没有匹配，就返回 false。

var hasPathSum = function(root, sum) {
    if(!root) return false;
    let res = false;
    const dfs = (n, s) => {
        // 如果为叶子节点进行判断
        if (!n.left && !n.right && s === sum) {
            res = true;
        }
        if (n.left) dfs(n.left, s + n.left.val);
        if (n.right) dfs(n.right, s + n.right.val);
    }
    dfs(root, root.val);
    return res;
};

遍历 json 的所有节点值

遍历 json 的每个节点的值：

const json = {
  a: {
    b: {
      c: '1'
    }
  },
  d: [1, 2],
}

const dfs = (n, path) => {
  console.log(n)
  if (n instanceof Object) {
    Object.keys(n).forEach(k => {
      dfs(n[k], path.concat(k))
    })
  }
}

dfs(json, [])

antd 中 tree 的渲染：

const json = [
  {
    title: '一',
    key: '1',
    children: [{title: '三', key: "3", children: [
      {
        title: '五',
        key: '5',
        children: [] 
      }
    ]}] 
  },
  {
    title: '二',
    key: '2',
    children: [{title: '四', key: "4", children: []}] 
  }
]

const Demo = () => {
  const dfs = (n) =>{
    return (
      <TreeNode title={n.title} key={n.key}>
        {
          n.children.map(dfs)
        }
      </TreeNode>
    )
  }
  return (
    <Tree>
      {
        json.map(dfs)
      }
    </Tree>
  )
}

阅读量：

评 论：