定义

• 堆是一种特殊的完全二叉树；

完全二叉树是每层节点都完全填满，在最后一层如果不是满的，则只缺少右边的若干节点。

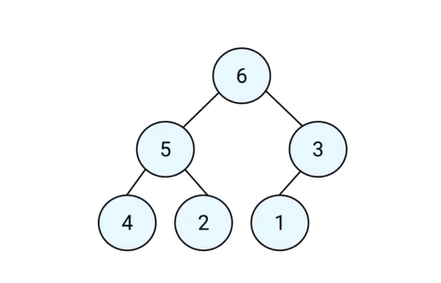
• 所有的节点都大于等于（最大堆）或小于等于（最小堆）他的子节点；

js 中的堆

• js 中通常用数组表示堆；

广度优先遍历：

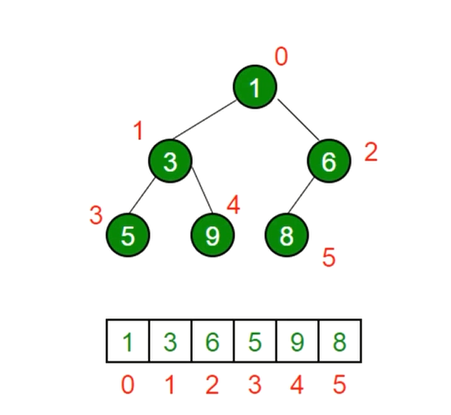
• 左侧子节点的位置是 2 * index + 1；
• 右侧子节点的位置是 2 * index + 2；
• 父节点位置是 (index - 1) / 2

堆的应用

• 堆能高效、快速地找出最大值和最小值，时间复杂度为 o(1)；

• 找出第 k 个最大(小)元素；

首先构建一个最小堆，并将元素依次插入堆中；当对的容量超过 k，就删除堆顶；插入结束后，堆顶就是第 k 个最大元素；

js 实现最小堆

主要是通过声明一个数组，然后实现插入、删除堆顶、获取堆顶、获取堆大小等方法。

插入

• 将值插入堆的底部，即数组的尾部；
• 然后上移：将这个值和他的父节点进行交换，直到父节点小于等于这个插入的值；
• 大小为 k 的堆中插入元素的时间复杂度为 O(logk)；

class MinHeap {
  constructor() {
    this.heap = []
  }

  getParentIndex(i) {
    // return Math.floor((i - 1) / 2)
    return (i - 1) >> 1
  }

  swap(i1, i2) {
    const temp = this.heap[i1]
    this.heap[i1] = this.heap[i2]
    this.heap[i2] = temp
  }

  shiftUp(index) {
    if (index === 0) return
    const parentIndex = this.getParentIndex(index)
    if (this.heap[parentIndex] > this.heap[index]) {
      // 交换值
      this.swap(parentIndex, index)
      // 继续上移操作
      this.shiftUp(parentIndex)
    }
  }

  insert(value) {
    this.heap.push(value)
    // 上移操作-参数为要插入值的数组的下标
    this.shiftUp(this.heap.length - 1)
  }
}

删除堆顶

• 用数组尾部元素替换堆顶（直接删除堆顶会破坏堆结构，因为数组的元素都会往前移动）；
• 然后下移：将新堆顶和他的子节点进行交换，直到子节点大于等于这个新堆顶；
• 大小为 k 的堆中删除堆顶的时间复杂度为 O(logk)；

class MinHeap {
  constructor() {
    this.heap = []
  }

  // 获取左侧子节点
  getLeftIndex(i) {
    return i * 2 + 1
  }

  // 获取右侧子节点
  getRightIndex(i) {
    return i * 2 + 2
  }

  swap(i1, i2) {
    const temp = this.heap[i1]
    this.heap[i1] = this.heap[i2]
    this.heap[i2] = temp
  }


  shiftDown(index) {
    const leftIndex = this.getLeftIndex(index)
    const rightIndex = this.getRightIndex(index)
    if (this.heap[leftIndex] < this.heap[index]) {
      // 交换位置
      this.swap(leftIndex, index)
      // 继续下移
      this.shiftDown(leftIndex)
    }

    if (this.heap[rightIndex] < this.heap[index]) {
      // 交换位置
      this.swap(rightIndex, index)
      // 继续下移
      this.shiftDown(rightIndex)
    }
  }

  pop() {
    this.heap[0] = this.heap.pop()
    // 进行下移操作-参数为从指定位置下移的下标
    this.shiftDown(0)
  }
}

获取堆顶和堆的大小

• 获取堆顶：返回数组的头部
• 获取堆的大小：返回数组的长度

class MinHeap {
  constructor() {
    this.heap = []
  }
  // 获取堆顶元素
  peek() {
    return this.heap[0]
  }

  // 获取堆大小
  size() {
    return this.heap.length
  }
}

整体代码：

class MinHeap {
  constructor() {
    this.heap = []
  }

  getParentIndex(i) {
    // return Math.floor((i - 1) / 2)
    return (i - 1) >> 1
  }

  // 获取左侧子节点
  getLeftIndex(i) {
    return i * 2 + 1
  }

  // 获取右侧子节点
  getRightIndex(i) {
    return i * 2 + 2
  }

  swap(i1, i2) {
    const temp = this.heap[i1]
    this.heap[i1] = this.heap[i2]
    this.heap[i2] = temp
  }

  shiftUp(index) {
    if (index === 0) return
    const parentIndex = this.getParentIndex(index)
    if (this.heap[parentIndex] > this.heap[index]) {
      // 交换值
      this.swap(parentIndex, index)
      // 继续上移操作
      this.shiftUp(parentIndex)
    }
  }

  shiftDown(index) {
    const leftIndex = this.getLeftIndex(index)
    const rightIndex = this.getRightIndex(index)
    if (this.heap[leftIndex] < this.heap[index]) {
      // 交换位置
      this.swap(leftIndex, index)
      // 继续下移
      this.shiftDown(leftIndex)
    }

    if (this.heap[rightIndex] < this.heap[index]) {
      // 交换位置
      this.swap(rightIndex, index)
      // 继续下移
      this.shiftDown(rightIndex)
    }
  }

  // 插入元素
  insert(value) {
    this.heap.push(value)
    // 上移操作-参数为要插入值的数组的下标
    this.shiftUp(this.heap.length - 1)
  }

  // 移除堆顶
  pop() {
    this.heap[0] = this.heap.pop()
    // 进行下移操作-参数为从指定位置下移的下标
    this.shiftDown(0)
  }

  // 获取堆顶元素
  peek() {
    return this.heap[0]
  }

  // 获取堆大小
  size() {
    return this.heap.length
  }
}

const h = new MinHeap()
h.insert(3)
h.insert(2)
h.insert(1)

使用场景

数组中的第K个最大元素

在未排序的数组中找到第 k 个最大的元素。请注意，你需要找的是数组排序后的第 k 个最大的元素，而不是第 k 个不同的元素。

示例 1:

输入: [3,2,1,5,6,4] 和 k = 2
输出: 5

https://leetcode-cn.com/problems/kth-largest-element-in-an-array/

• 解题思路：使用堆来解决；
• 解题步骤：首先构建一个最小堆，并依次把数组的值插入堆中；当堆的容量超过 k，就删除堆顶；插入结束后，堆顶就是 k 个最大元素；

/**
 * @param {number[]} nums
 * @param {number} k
 * @return {number}
 */

class MinHeap {
  constructor() {
    this.heap = []
  }

  getParentIndex(i) {
    // return Math.floor((i - 1) / 2)
    return (i - 1) >> 1
  }

  // 获取左侧子节点
  getLeftIndex(i) {
    return i * 2 + 1
  }

  // 获取右侧子节点
  getRightIndex(i) {
    return i * 2 + 2
  }

  swap(i1, i2) {
    const temp = this.heap[i1]
    this.heap[i1] = this.heap[i2]
    this.heap[i2] = temp
  }

  shiftUp(index) {
    if (index === 0) return
    const parentIndex = this.getParentIndex(index)
    if (this.heap[parentIndex] > this.heap[index]) {
      // 交换值
      this.swap(parentIndex, index)
      // 继续上移操作
      this.shiftUp(parentIndex)
    }
  }

  shiftDown(index) {
    const leftIndex = this.getLeftIndex(index)
    const rightIndex = this.getRightIndex(index)
    if (this.heap[leftIndex] < this.heap[index]) {
      // 交换位置
      this.swap(leftIndex, index)
      // 继续下移
      this.shiftDown(leftIndex)
    }

    if (this.heap[rightIndex] < this.heap[index]) {
      // 交换位置
      this.swap(rightIndex, index)
      // 继续下移
      this.shiftDown(rightIndex)
    }
  }

  // 插入元素
  insert(value) {
    this.heap.push(value)
    // 上移操作-参数为要插入值的数组的下标
    this.shiftUp(this.heap.length - 1)
  }

  // 移除堆顶
  pop() {
    this.heap[0] = this.heap.pop()
    // 进行下移操作-参数为从指定位置下移的下标
    this.shiftDown(0)
  }

  // 获取堆顶元素
  peek() {
    return this.heap[0]
  }

  // 获取堆大小
  size() {
    return this.heap.length
  }
}

var findKthLargest = function(nums, k) {
    const h = new MinHeap();
    nums.forEach(n => {
        h.insert(n)
        // 堆中元素超过 k
        if (h.size() > k) {
            // 移除堆顶元素
            h.pop();
        }
    });
    return h.peek()
};

前 K 个高频元素

给定一个非空的整数数组，返回其中出现频率前 k 高的元素。

示例 1:

输入: nums = [1,1,1,2,2,3], k = 2
输出: [1,2]

https://leetcode-cn.com/problems/top-k-frequent-elements/

提示：

• 你可以假设给定的 k 总是合理的，且 1 ≤ k ≤ 数组中不相同的元素的个数。
• 你的算法的时间复杂度必须优于 O(n log n) , n 是数组的大小。
• 题目数据保证答案唯一，换句话说，数组中前 k 个高频元素的集合是唯一的。
• 你可以按任意顺序返回答案。

代码：

class MinHeap {
  constructor() {
    this.heap = []
  }

  getParentIndex(i) {
    // return Math.floor((i - 1) / 2)
    return (i - 1) >> 1
  }

  // 获取左侧子节点
  getLeftIndex(i) {
    return i * 2 + 1
  }

  // 获取右侧子节点
  getRightIndex(i) {
    return i * 2 + 2
  }

  swap(i1, i2) {
    const temp = this.heap[i1]
    this.heap[i1] = this.heap[i2]
    this.heap[i2] = temp
  }

  shiftUp(index) {
    if (index === 0) return
    const parentIndex = this.getParentIndex(index)
    if (this.heap[parentIndex] && this.heap[parentIndex].value > this.heap[index].value) {
      // 交换值
      this.swap(parentIndex, index)
      // 继续上移操作
      this.shiftUp(parentIndex)
    }
  }

  shiftDown(index) {
    const leftIndex = this.getLeftIndex(index)
    const rightIndex = this.getRightIndex(index)
    if (this.heap[leftIndex] && this.heap[leftIndex].value < this.heap[index].value) {
      // 交换位置
      this.swap(leftIndex, index)
      // 继续下移
      this.shiftDown(leftIndex)
    }

    if (this.heap[rightIndex] && this.heap[rightIndex].value < this.heap[index].value) {
      // 交换位置
      this.swap(rightIndex, index)
      // 继续下移
      this.shiftDown(rightIndex)
    }
  }

  // 插入元素
  insert(value) {
    this.heap.push(value)
    // 上移操作-参数为要插入值的数组的下标
    this.shiftUp(this.heap.length - 1)
  }

  // 移除堆顶
  pop() {
    this.heap[0] = this.heap.pop()
    // 进行下移操作-参数为从指定位置下移的下标
    this.shiftDown(0)
  }

  // 获取堆顶元素
  peek() {
    return this.heap[0]
  }

  // 获取堆大小
  size() {
    return this.heap.length
  }
}

/**
 * @param {number[]} nums
 * @param {number} k
 * @return {number[]}
 */
var topKFrequent = function(nums, k) {
    const map = new Map();
    nums.forEach(n => {
        map.set(n, map.has(n) ? map.get(n) + 1 : 1);
    });
    const h = new MinHeap();
    map.forEach((value, key) => {
        h.insert({value, key});
        if (h.size() > k) {
            h.pop();
        }
    });
    return h.heap.map(a => a.key)
};

合并 K 个升序链表

给你一个链表数组，每个链表都已经按升序排列。

请你将所有链表合并到一个升序链表中，返回合并后的链表。

示例 1：

输入：lists = [[1,4,5],[1,3,4],[2,6]]
输出：[1,1,2,3,4,4,5,6]
解释：链表数组如下：
[
  1->4->5,
  1->3->4,
  2->6
]
将它们合并到一个有序链表中得到。
1->1->2->3->4->4->5->6

链接：https://leetcode-cn.com/problems/merge-k-sorted-lists

• 解题思路：新链表的下一个节点一定是 k 个链表头中的最小节点；使用堆来解决；
• 解题步骤：构建一个最小堆，并依次把链表头插入堆中；然后弹出堆顶接到输出链表，并将堆顶所在链表的新链表头插入堆中；等堆元素全部弹出，合并工作就完成了。

class MinHeap {
  constructor() {
    this.heap = []
  }

  getParentIndex(i) {
    // return Math.floor((i - 1) / 2)
    return (i - 1) >> 1
  }

  // 获取左侧子节点
  getLeftIndex(i) {
    return i * 2 + 1
  }

  // 获取右侧子节点
  getRightIndex(i) {
    return i * 2 + 2
  }

  swap(i1, i2) {
    const temp = this.heap[i1]
    this.heap[i1] = this.heap[i2]
    this.heap[i2] = temp
  }

  shiftUp(index) {
    if (index === 0) return
    const parentIndex = this.getParentIndex(index)
    if (this.heap[parentIndex] && this.heap[parentIndex].val > this.heap[index].val) {
      // 交换值
      this.swap(parentIndex, index)
      // 继续上移操作
      this.shiftUp(parentIndex)
    }
  }

  shiftDown(index) {
    const leftIndex = this.getLeftIndex(index)
    const rightIndex = this.getRightIndex(index)
    if (this.heap[leftIndex] && this.heap[leftIndex].val < this.heap[index].val) {
      // 交换位置
      this.swap(leftIndex, index)
      // 继续下移
      this.shiftDown(leftIndex)
    }

    if (this.heap[rightIndex] && this.heap[rightIndex].val < this.heap[index].val) {
      // 交换位置
      this.swap(rightIndex, index)
      // 继续下移
      this.shiftDown(rightIndex)
    }
  }

  // 插入元素
  insert(value) {
    this.heap.push(value)
    // 上移操作-参数为要插入值的数组的下标
    this.shiftUp(this.heap.length - 1)
  }

  // 移除堆顶
  pop() {
    if(this.size() === 1) return this.heap.shift()
    const top = this.heap[0]
    this.heap[0] = this.heap.pop()
    // 进行下移操作-参数为从指定位置下移的下标
    this.shiftDown(0)
    return top
  }

  // 获取堆顶元素
  peek() {
    return this.heap[0]
  }

  // 获取堆大小
  size() {
    return this.heap.length
  }
}

/**
 * Definition for singly-linked list.
 * function ListNode(val, next) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.next = (next===undefined ? null : next)
 * }
 */
/**
 * @param {ListNode[]} lists
 * @return {ListNode}
 */
var mergeKLists = function(lists) {
    // 输出链表
    const res = new ListNode(0);
    let p = res;
    const h = new MinHeap();
    // 将链表中的头部插入到堆中
    lists.forEach(l => {
        if (l) h.insert(l)
    });
    while(h.size()) {
        // 获取所有链表头部
        const n = h.pop();
        p.next = n;
        p = p.next;
        if (n.next) h.insert(n.next);
    }
    return res.next;
};