# 定义
- 图是网络结构的抽象模型,是一组由边连接的节点。
- 使用图可以表示道路、航班以及通信等数据。
- js 中通过 object 和 array 构建。
# 图的表示
# 临接矩阵
图最常见的实现是邻接矩阵。每个节点都和一个整数相关联,该整数将作为数组的索引。
下图是表示两个点是否相连,0 表示不相连,1 表示相连。
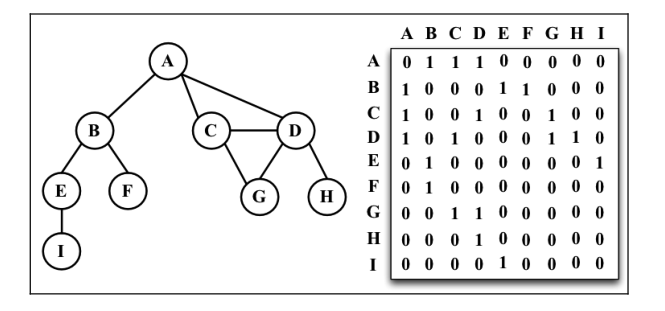
# 临接表
可以使用邻接表的动态数据结构来表示图。邻接表由图中每个顶点的相邻顶点列表所组成。
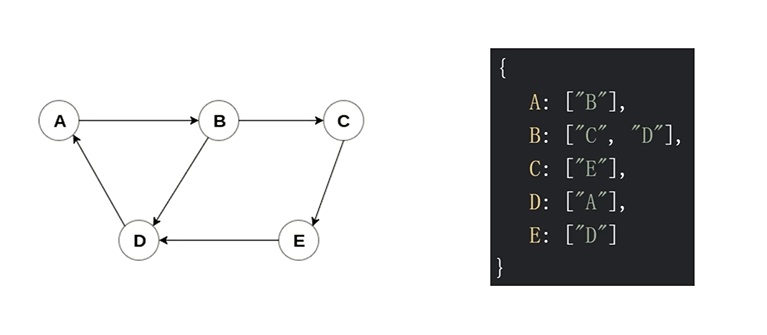
# 关联矩阵
在关联矩阵中,矩阵的行表示顶点,列表示边。如下图所示,使用二维数组来表示两者之间的连通性,如果顶点 v是边 e的入射点,则 array[v][e] === 1;否则, array[v][e] === 0 。
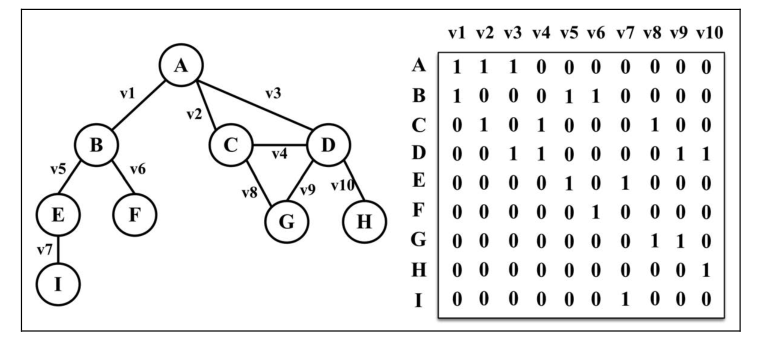
关联矩阵通常用于边的数量比顶点多的情况,以节省空间和内存。
# 图的深度、广度优先遍历
# 深度优先遍历
尽可能深的搜索图的分支;
深度优先遍历算法有以下要点:
- 访问根节点;
- 对根节点的
没访问过的相邻节点挨个进行深度优先遍历;
之所以添加没有访问过的限定是防止如下图的 0 与 2 ,之间进入不限的循环。加上限定条件如右侧图的 0 与 2,首先 2 访问 0,再次 0 访问 2 时,不会执行。因为之前已经遍历过。
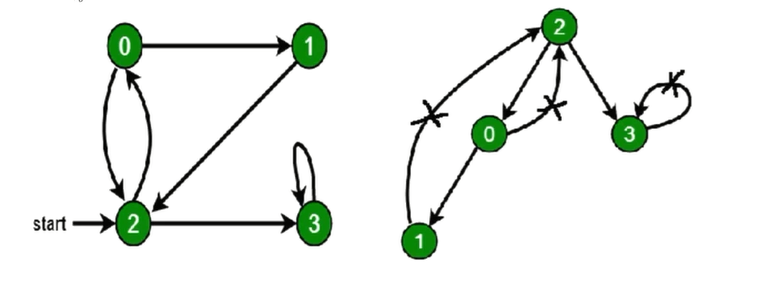
- 代码示例
下面代码是通过临接表的表示法表示的一个图数据
// graphic.js
const graphic = {
0: [1, 2],
1: [2],
2: [0, 3],
3: [3]
}
module.exports = graphic
const graphic = require('./graphic')
// 记录访问过的节点
const visited = new Set()
const dfs = (n) => {
// 访问根节点
console.log(n)
visited.add(n)
// 对没有访问过的相邻节点挨个进行深度优先遍历
graphic[n].forEach(c => {
if (!visited.has(c)) {
dfs(c)
}
})
}
dfs(2)
# 广度优先遍历
先访问离根节点最近的节点。
广度优先遍历算法有以下要点:
新建一个队列,把跟节点入对;
把对头出队并访问;
把对头的
没访问过的相邻节点入队;重复第二、三步,直到队列为空;
代码示例
const graphic = require('./graphic')
const visited = new Set()
visited.add(2)
const q = [2]
while(q.length) {
const n = q.shift()
console.log(n)
graphic[n].forEach(c => {
if (!visited.has(c)) {
q.push(c)
visited.add(n)
}
})
}
# 使用场景
# 有效数字
验证给定的字符串是否可以解释为十进制数字。
例如:
"0" => true
" 0.1 " => true
"abc" => false
"1 a" => false
"2e10" => true
" -90e3 " => true
" 1e" => false
"e3" => false
" 6e-1" => true
" 99e2.5 " => false
"53.5e93" => true
" --6 " => false
"-+3" => false
"95a54e53" => false
链接:https://leetcode-cn.com/problems/valid-number
- 解题思路:如下图,每个状态是可以变换的 0 为空字符串或者数字 0,如果后面跟 +/- 就抓换为 1 状态;以此类推,最后查看最终状态是否为图中对应 3、6、5 状态即有效。
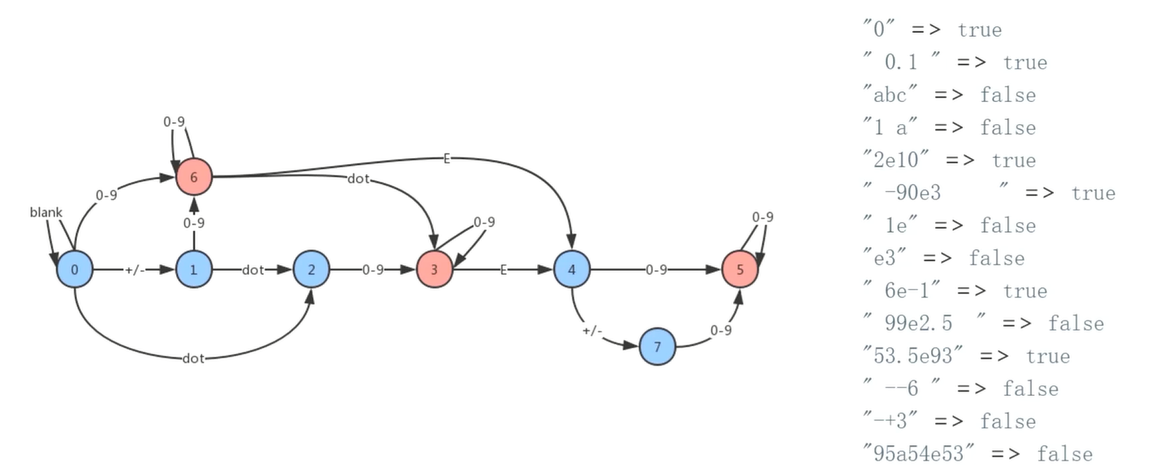
- 解题步骤:首先构建一个表示状态的图,然后遍历字符串,并沿着图走,如果到了某个节点无路可走就返回 false;遍历结束,如走到 3、6、5 状态,就返回 true,否则返回 false。
/**
* @param {string} s
* @return {boolean}
*/
var isNumber = function(s) {
// 构建图
const graph = {
0: { 'black': 0, 'sign': 1, '.': 2, 'digit': 6 },
1: { 'digit': 6, '.': 2},
2: { 'digit': 3 },
3: { 'digit': 3, 'e': 4 },
4: { 'digit': 5, 'sign': 7 },
5: { 'digit': 5 },
6: { 'digit': 6, '.': 3, 'e': 4 },
7: { 'digit': 5 }
};
// 遍历字符串
let state = 0;
for (c of s.trim()) {
if (c >= '0' && c <= '9') {
c = 'digit';
} else if (c === '') {
c = 'black';
} else if (c === '+' || c === '-') {
c = 'sign';
}
// 获取新的状态
state = graph[state][c];
if (state === undefined) {
return false
}
}
if (state === 3 || state === 5 || state === 6) {
return true
}
return false
};
# 太平洋大西洋水流问题(DEM 找山脊线)
给定一个 m x n 的非负整数矩阵来表示一片大陆上各个单元格的高度。“太平洋”处于大陆的左边界和上边界,而“大西洋”处于大陆的右边界和下边界。
规定水流只能按照上、下、左、右四个方向流动,且只能从高到低或者在同等高度上流动。
请找出那些水流既可以流动到“太平洋”,又能流动到“大西洋”的陆地单元的坐标。
提示:
输出坐标的顺序不重要
m 和 n 都小于150
示例:
给定下面的 5x5 矩阵:
太平洋 ~ ~ ~ ~ ~
~ 1 2 2 3 (5) *
~ 3 2 3 (4) (4) *
~ 2 4 (5) 3 1 *
~ (6) (7) 1 4 5 *
~ (5) 1 1 2 4 *
* * * * * 大西洋
返回:
[[0, 4], [1, 3], [1, 4], [2, 2], [3, 0], [3, 1], [4, 0]] (上图中带括号的单元).
链接:https://leetcode-cn.com/problems/pacific-atlantic-water-flow
- 解题思路:将矩阵可以想象成一个图数据结构,从海岸线逆流而上遍历图所到之处就是可以流到某个大洋的坐标。
- 解题步骤:新建两个矩阵,分别记录能流到两个大洋的坐标;然后从海岸线,多管齐下,同时深度优先遍历图,过程中填充上述矩阵;然后遍历两个矩阵,找出能流到两个大洋的坐标。
/**
* @param {number[][]} matrix
* @return {number[][]}
*/
var pacificAtlantic = function(matrix) {
if(!matrix || !matrix[0]) return [];
// 新建两个矩阵
const m = matrix.length; // 行
const n = matrix[0].length; // 列
const flow1 = Array.from({ length: m }, () => new Array(n).fill(false))
const flow2 = Array.from({ length: m }, () => new Array(n).fill(false))
// 深度优先遍历
// 参数为 行、列、矩阵
const dfs = (r, c, flow) => {
flow[r][c] = true;
// 遍历相邻节点-上下左右
[[r-1, c], [r + 1, c], [r, c - 1], [r, c + 1]].forEach(([nr, nc]) => {
if (
// 保证在矩阵中
nr >= 0 && nr < m &&
nc >= 0 && nc < n &&
// 没有访问过的节点
!flow[nr][nc] &&
// 保证逆流而上,下一个节点大于等于上一个节点
matrix[nr][nc] >=matrix[r][c]
) {
dfs(nr, nc, flow)
}
});
}
// 沿着海岸线逆流而上
for(let r = 0; r < m; r+=1) {
dfs(r, 0, flow1);
dfs(r, n-1, flow2);
}
for(let c = 0; c < n; c+=1) {
dfs(0, c, flow1);
dfs(m - 1, c, flow2);
}
// 判断可以流到两个大洋的坐标
const res = [];
for (let r = 0; r < m; r+=1) {
for (let c = 0; c < n; c+=1) {
if (flow1[r][c] && flow2[r][c]) {
res.push([r, c]);
}
}
}
return res;
};
# 克隆图
给你无向连通图中一个节点的引用,请你返回该图的深拷贝克隆)。图中的每个节点都包含它的值 val(int) 和其邻居的列表(list[Node])。
测试用例格式:
简单起见,每个节点的值都和它的索引相同。例如,第一个节点值为 1(val = 1),第二个节点值为 2(val = 2),以此类推。该图在测试用例中使用邻接列表表示。 邻接列表是用于表示有限图的无序列表的集合。每个列表都描述了图中节点的邻居集。 给定节点将始终是图中的第一个节点(值为 1)。你必须将 给定节点的拷贝 作为对克隆图的引用返回。
https://leetcode-cn.com/problems/clone-graph/
解题思路:拷贝所有节点以及拷贝各个节点之间的关系,也就是拷贝所有边;
解题步骤:深度或广度优先遍历所有节点,然后拷贝所有的节点,存储起来。将拷贝的节点,按照原图的连接方法进行连接。
深度优先遍历算法:
/**
* // Definition for a Node.
* function Node(val, neighbors) {
* this.val = val === undefined ? 0 : val;
* this.neighbors = neighbors === undefined ? [] : neighbors;
* };
*/
/**
* @param {Node} node
* @return {Node}
*/
var cloneGraph = function(node) {
if (!node) return;
const visited = new Map();
const dfs = (n) => {
const nCopy = new Node(n.val);
// 拷贝节点
visited.set(n, nCopy);
(n.neighbors || []).forEach(ne => {
if (!visited.has(ne)) {
dfs(ne);
}
nCopy.neighbors.push(visited.get(ne));
});
};
dfs(node);
return visited.get(node);
};
- 广度优先遍历算法:
/**
* @param {Node} node
* @return {Node}
*/
var cloneGraph = function(node) {
if (!node) return;
const visited = new Map();
const q = [node];
visited.set(node, new Node(node.val));
while(q.length) {
const n = q.shift();
(n.neighbors || []).forEach(ne => {
if (!visited.has(ne)) {
q.push(ne);
visited.set(ne, new Node(ne.val));
}
visited.get(n).neighbors.push(visited.get(ne));
})
}
return visited.get(node);
};